Глазковые диаграммы и BER(bit error rate)

Для анализа высокочастотных цифровых схем часто применяются глазковые диаграммы, в этой статье описаны базовые принципы построения глазковых диаграмм и как с помощью них получить информацию о дефектах в спроектированной системе. Так же поговорим о недостатках данного метода измерения и что применяется для анализа по мимо глазковых диаграмм.

Глазковая диаграмма

Для начала необходимо понять, как же строится глазковая диаграмма.
Типичная диаграмма выглядит следующим образом(источник):

Построение глазковой диаграммы

Для построения диаграммы не обязательно иметь дифференциальный сигнал, её вполне можно построить и с помощью single ended сигнала. Для построения глаза необходимо через тракт прогнать определённую последовательность, которая сформирует картину, похожую как на рисунке сверху.

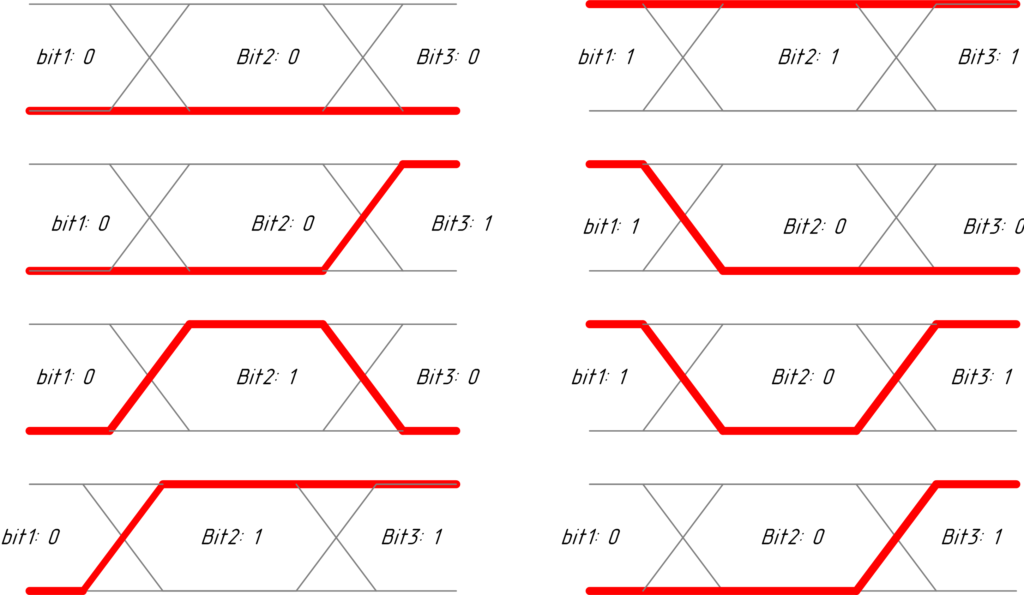
Рассмотрим минимальный набор информации, которая должна пройти через тракт, для построения глаза.

Теперь мысленно просуммируем все последовательности и получим:

Осциллограф, накапливает данные, наслаивая их друг на друга, и в результате получаем что то похоже, как на рисунке в начале статьи.

Визуальный анализ глазковой диаграммы

Вернёмся к реальным диаграммам и возьмём для примера эту(источник):

Что мы тут видим:

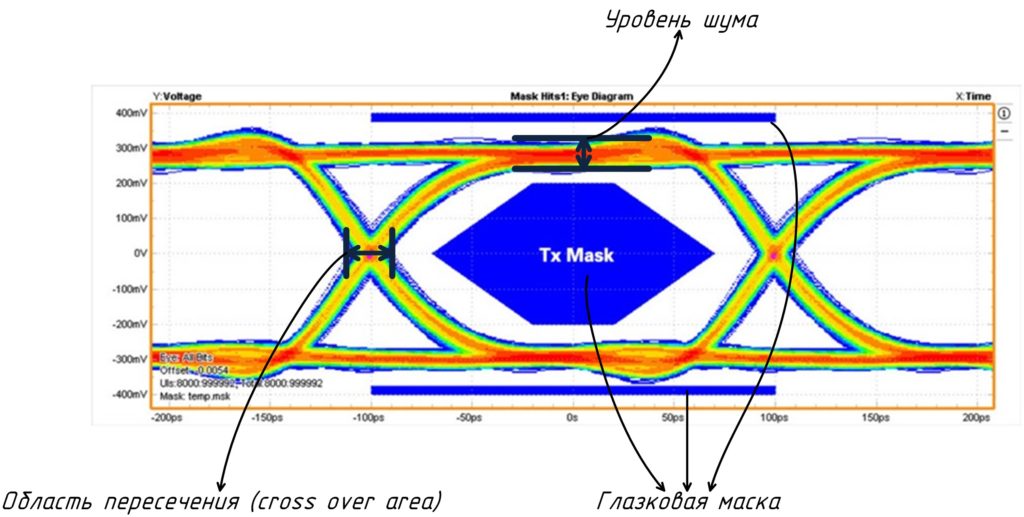
Глазковая маска(eye mask) — по сути некий паттерн который можно задать в настройках осциллографа, для вывода вместе с диаграммой. Зачем он нужен? Всё очень просто, ряд стандартных интерфейсов имеют требования по качеству цифрового тракта на разных концах линии передач(например у передатчик и у приёмника, до кабеля и после). Для определения качества тракта, задаётся некая строго определённая маска(а если быть конкретнее точки для её построения) в пределы которой не должен попадать ни один сигнал из той выборки. Например, по рисунку выше, можно сказать, что тест пройден успешно.

А вот пример с явными проблемами(источник):

Как видно, сигнал касается и пересекает маску, и по этому делается вывод о некачественном цифровом тракте.

Примеры точек для задания маски в глазковой диаграмме можно посмотреть в спецификации USB, параграф «High-speed Signaling Eye Patterns and Rise and Fall Time».

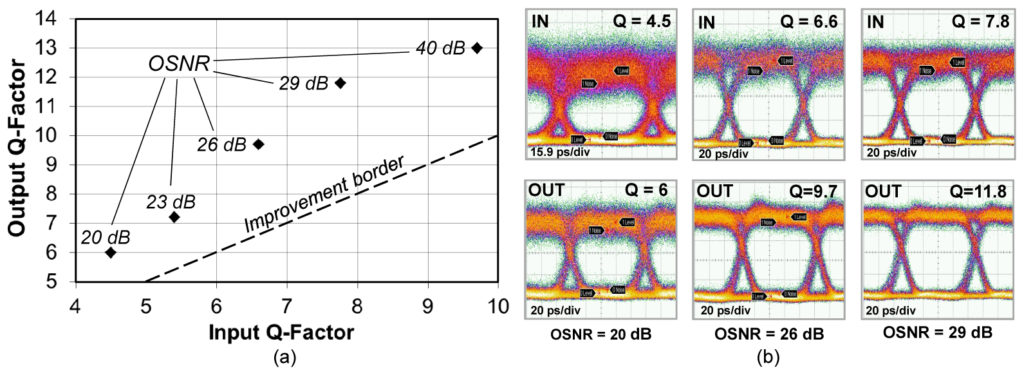
Уровень шума(noise amplitude) — это толщина отрисованной линии на осциллографе в тех временных областях, где закончились переходные процессы, или другими словами, там где сигнал может быть чётко определён (0 или 1). Чаще данный параметр используется для расчёта других показателей, которые считаются осциллографом автоматически. Например, добротность(Q-factor). Если коротко, то чем ниже Qf, тем хуже качество глазговской диаграммы. Вот наглядный пример(источник):

Иногда в литературе можно встретить параметр SNR, но это тоже самой что и добротность в глазковых диаграммах.

Дрожание и cross over area — в глазковой диаграмме дрожание можно определить по толщине области пересечения (cross over area). Понятное дело, что чем данная область тоньше, тем лучше. Но есть несколько нюансов.

Один из нюансов заключается в следующем: желательное пересечение фронтов всегда происходило на центральной оси глаза, как показано на рисунке ниже.

Причина по которой может происходить пересечение не в центре, это разбаланс драйвера, при котором время длительности логической 1 превышает время длительности логического нуля(или на оборот). Ниже приведён наглядный пример c пересечением в центре(слева) и пересечением выше центральной оси(справа). Берём две последовательности сигнала где логическая 1 по времени превышает логический 0 и получаем Cross over 80%.

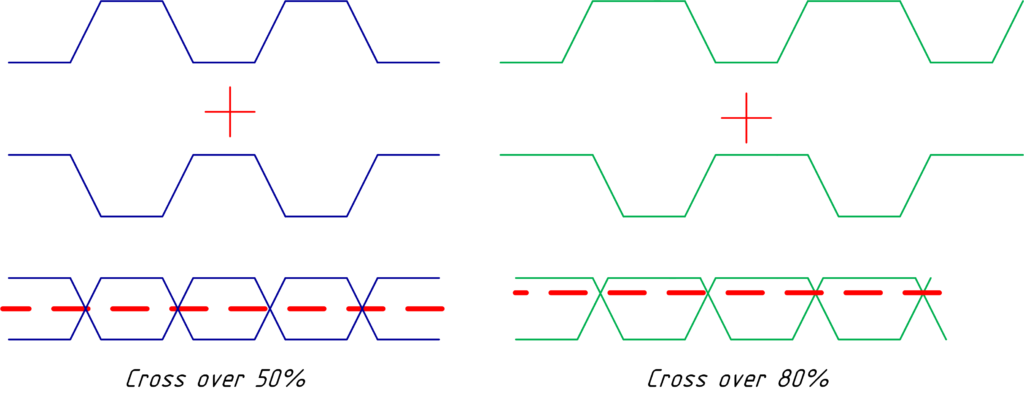
Второй нюанс — плотность дрожания должна возрастать без перепадов к центру пересечения нарастающих и спадающих фронтов. Если ещё раз обратить внимание на диаграмму ниже, видно как в центре, диаграмма имеет ярко выраженный красный цвет, хотя по краям жёлтый, перетекающий в синий.

Оценка характера возрастания плотности пересечений в cross over области по цвету является весьма поверхностным анализом. Для этого специально придумали метрику/метод измерения — bit error rate(BER), поговорим о нём подробнее в следующем параграфе.

Анализ глазковой диаграммы с помощью Bit Error Rate

Основы

BER это число, которое показывает отношение бит принятых с ошибкой к общему числу отправленных бит данных:

\LARGE BER = \frac{error \,\, bit}{all \,\, bit}

Обычно показатель используется для оценки качество сетевого трафика и имеет значения 10 в -9..-12 степени. Но так же данный подход можно применять для исследования глазковой диаграммы.

Анализ

Как уже писалось выше, BER можно использовать для исследования глаза в областях пересечения, а если быть точнее, то исследование сводится к изучения характеристик джиттера. Давайте рассмотрим область пересечения ближе, держа в уме формулу для определения BER. Представим, что мы отсняли глазковую диаграмму, далее в произвольное место вблизи пересечения помещаем точку в которой будет считаться BER. Вот например как тут:

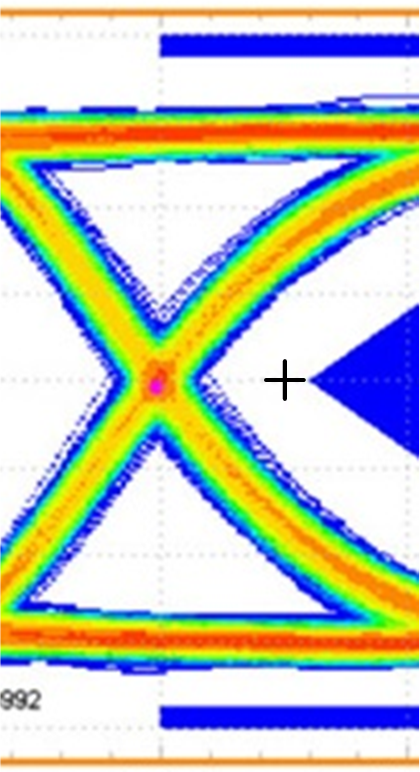
Понятно, что в точке как на рисунке выше BER = 0. Интересующая нас область находится левее. Будем двигать точку влево, до тех пор пока не найдём такое положение, где BER = 1.

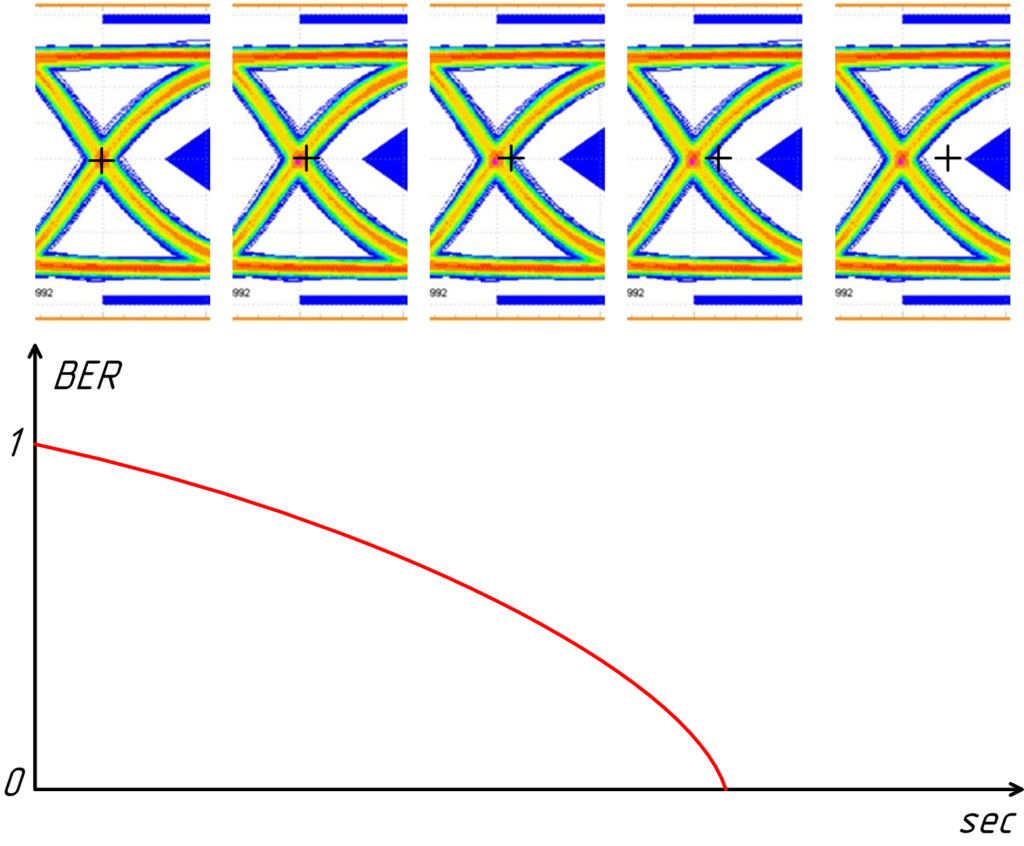
Если кривая BER не имеет локальных максимумов/минимумов, можно говорить о том, что нет аномалий в джиттере.

Точно такое же необходимо провести для второго края, в данном случае правого пересечения. В идеале, зависимость BER должна быть одинакова с обоих краёв, как на рисунке ниже(источник):

Недостаток глазковых диаграмм в анализе качества цифрового тракта.

При отрисовки глазковой диаграммы, как правило используется небольшое число бит, одна из основных причин — это память осциллографа. Если рассматривать возникновение ошибки с точки зрения вероятности, то становится очевидно — чем меньше число бить, тем сложнее обнаружить редкую ошибку.

Глазковая диаграмма хорошо подходит для быстрой оценки цифрового тракта, с целью выявления грубых ошибок в проектирование. Но например, доказать с помощью глазковой диаграммы надёжность системы в которой количество ошибочно принятых бит(ERR_bit) данных меньше какой то константы, будет затруднительно. Особенно, когда ERR_bit -> 0. С данной задачей хорошо справится Bit Error Rate Test(BERT) в основе которого лежит параметр BER. Об этом дальше и пойдёт речь.

Bit Error Rate Test

В основе Bit Error Rate Test лежит измерение параметра BER. Как посчитать BER выше уже писалось, но повторение мать учения.

BER это число, которое показывает отношение бит принятых с ошибкой к общему числу отправленных бит:

\LARGE BER = \frac{error \,\, bit}{all \,\, bit}

Обычно показатель используется для оценки качество сетевого трафика и имеет значения 10 в -9..-12 степени.

Постановка задачи.

Предположим у нас есть железка с высокоскоростным интерфейсом. Необходимо проверить качество передачи по цифровому каналу. Обычно задаются конкретным верхним порогом BER, и проверяют превышает ли конкретный образец заранее заданное значение верхнего порога BER.

Когда речь идёт о малых количествах ошибок при большом трафике, можно сказать, что возникновение ошибки в тот или иной момент времени имеет вероятностный характер. Для нас это означает следующие: нельзя взять железку, подключить измерительное оборудование, запустить тест, поковырять в носу и остановить тест зафиксировав значение BER. Почему нельзя? А нельзя потому, что возможно передалось слишком малое количество бит за отведённый промежуток времени, и из за низкой вероятности появления ошибок, они толком не успели появится, и тест покажет отличный BER.

Допустим мы выяснили — лучше подождать подольше, тогда измерительный стенд выдаст BER, максимально приближенный к реальности. Это допустимо? Да, но только когда у вас одна железка и вагон времени… Что делать с большой партией которую необходимо проверить? Об этом поговорим в следующем параграфе.

Определение времени тестирование или какое количество бит передать через цифровой канал?

Мы принимаем тот факт, что появление ошибки для нас являются случайной величиной. Раз так, то в дальнейшем, мы будем рассматривать данный вопрос с точки зрения теории вероятности. Для удобства введём такое понятие как статистический уровень доверия (в литературе встречается как SLC).

Статистический уровень доверия — это вероятность, что фактическая вероятность больше чем некая константа, которую мы задали.

Фактическая вероятность — вероятность которая была получена при очень большом количестве(стремящимся к бесконечности) экспериментов.

Немного забегая вперёд, SLC по сути показывает, на сколько мы можем доверять нашей вероятности появления ошибок(BER) при определённом количестве тестов. Мы будем задавать разный уровень доверия, и наблюдать как меняется количество бит, которые необходимо передать в ходе тестирования.

Итак, все расчёты будут вестись на основе биномиального распределения. По сути биномиального распределение — это распределение вероятностей возникновения какого либо события n раз. Сразу для примера, построим биномиальное распределение вероятностей встретить n ошибочных битов при передачи 10^{9} бит в системе, вероятность ошибки 10^{-8} .

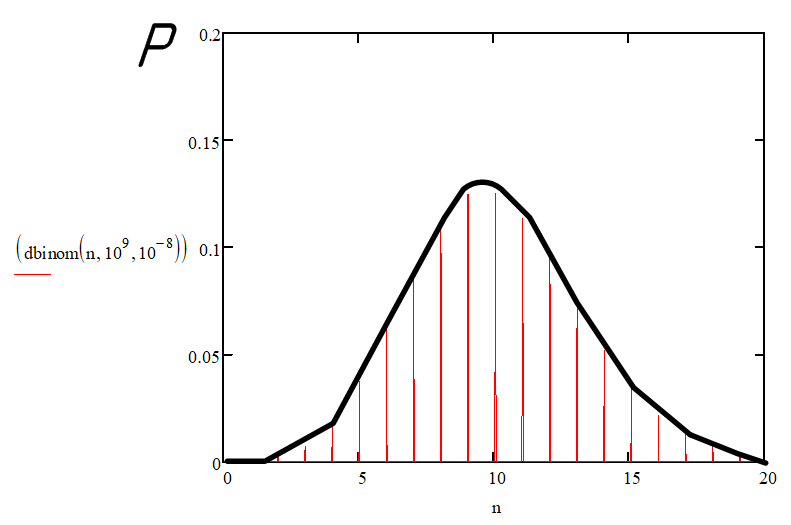
Из рисунка видно, что вероятность встретить 0 ошибочных бит как и 20 очень мала. А вот максимальная вероятность приходится на n = 10.

Опишем, что скрывается за функцией dbinom. Данная функция, для каждого n, считает вероятность по формуле Бернули:

\LARGE P = С_{k}^{m}\cdot p^{k} \cdot q^{m-k}

Где P — Вероятность, что в k независимых испытаний, некое случайное событие наступит ровно m раз. В случае биномиального распределения, данное событие считается для каждого m.
p — вероятность наступления событие единичной попытки.
q — вероятность, что событие не наступит при единичной попытки. Для q верно: q = 1-p.

Тут надо отметить, что если мы возьмём и посчитаем вероятности для большого числа k, и просуммируем их, то получим 1(ну или число очень близкое к 1). Изобразим это на графике:

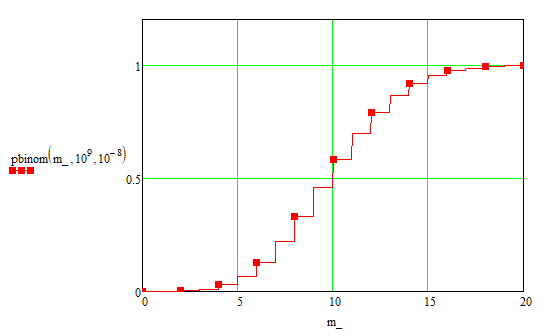
График выше можно читать следующем образом: вероятность того, что мы обнаружим 15 бит или меньше при передаче 10^{9} бит равна примерно 90%.

Теперь ещё раз вспомним постановку задачи. Нам необходимо найти количество бит, которые нужно передать, чтобы наш BER был близок к истинному BER. Держа это в уме, и что функция pbinom возвращает вероятность встретить m ошибок или менее. Можно сказать, что 1 — pbinom = SLC. Для наглядности построим всё это на одном графике.

Теперь мы говорим, что для SLC = 95%, нас устраивает если на 5 ошибочных битов приходилась почти вся вероятность(красный график). В данном графике это не так, поскольку мы передали через систему слишком маленькое количество бит. Давайте увеличим количество переданных бит.

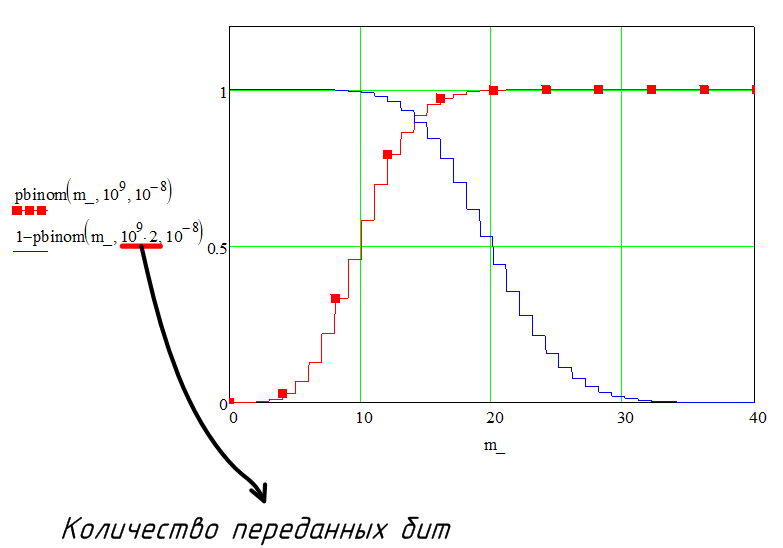
Теперь SLC = 95% нас удовлетворяет т.к. в него укладывается почти все возможные m.

Теперь запишем всё это математически, при этом я опустил вывод формулы для n(количество необходимых бит). Скажу лишь, что при вычисление допустимо применять теорему Пуассона. Формула для n выглядит следующим образом:

\LARGE n = \frac{1}{BER} \cdot (-ln(1-SLC))

Это уравнение справедливо для количества найденных ошибок равно 0(полное уравнение по ссылке). Почему 0? Всё очень просто, обычно у правильно спроектированной системы BER является на порядок ниже, чем того требует стандарт. Поэтому в этом уравнение, BER задаётся стандартом, и т.к. мы предполагаем что в тестируемой системе BER ниже, чем того требует стандарт, следовательно вероятность обнаружить 0 ошибок действительно велика.

Теперь давайте предположим, что нам необходимо подтвердить, что наша система удовлетворяет BER = 10^{-12} с SLC = 98%. В таком случае n = 3.9 \cdot 10^{12} бит будет достаточно. И если данные требования предъявляются для системы с скоростью передачи 1ГБит/с тогда время тестирования составить примерно 3900 секунд.

Реально ли серийные образцы тестируют так долго? Конечно же нет, если тестирование получается таким долгим, то в сигнал намеренно добавляют шум, чтобы увеличить BER и уменьшить время тестирования. Но это уже отдельная тема, здесь мы её касаться не будем.

Итог

Глазвовая диаграмма простой метод тестирования и анализа цифрового тракта, который позволяет выявлять грубые ошибки в проектирование.

Для более точного оценки качества системы коммуникации используют параметр BER, для данного теста необходимо более дорогостоящие оборудование и большое время на тестирование одного образца, но тем не менее есть методики, которые поваляют сократить время тестирования. При BER тестах, необходимо аккуратно подходить к выбору времени тестированию одного образца т.к. в случае неправильного выборе времени, можно сделать неправильный вывод о качестве изделия.