Параллельный и последовательный резонанс в RLC цепях.

Резонанс является одним из ключевых свойств RLC цепи. Понимание механизмов возникновения резонанса, а так же умение описать это явление в аналитическом виде, важно не только для схемотехника, но и для тополога печатных плат. То о чём будет написано в статье является базовыми понятиями, но считаю не будет лишним ещё раз проговорить о резонансе дабы освежить, возможно забытые, знания.

Последовательный резонанс RLC

Рассмотрим схему последовательного резонатора.

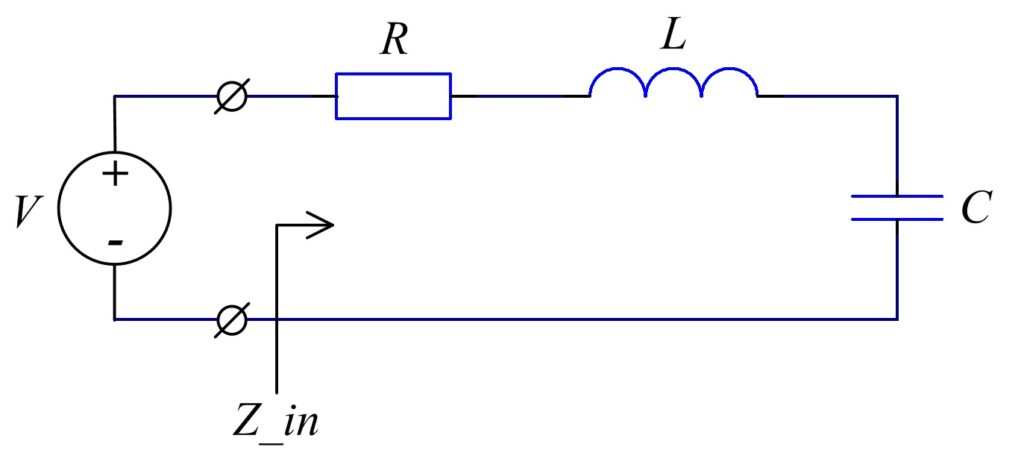
Как уже видно из схемы для описания нам понадобиться записать уравнение входного импеданса.

\Large Z_{in} = R + jwL - j\frac{1}{wC} (1)

Далее, для понимания происходящих процессов, удобно работать с мощностями. Запишем полную мощность в RLC цепи

\Large P = V_{rms} \cdot I_{rms} = \frac{V \cdot I}{ \sqrt{2}\cdot \sqrt{2}} = \frac{V \cdot I}{2} (2)

В уравнение фигурирует корень из двух, поскольку используется действующее значение переменного тока и напряжения.

Теперь запишем мощность в комплексной форме через импеданс из уравнения (1).

\Large P=\frac{I^{2}Z_{in} }{2}= \frac{1}{2} I^{2} \cdot (R + jwL - j\frac{1}{wC})

Раскроем скобки

\Large P=\frac{1}{2} I^{2}R + \frac{1}{2} I^{2}jwL - \frac{1}{2} I^{2}\frac{j}{wC} (3)

На этом моменте остановимся и внимательно посмотрим, что мы получили.

Для большей очевидности распишем каждую мощность, энергию используя среднеквадратическое (оно же действующие) значение тока или напряжения.

Напомним, что действующее значение для синусоидального сигнала находится как:

\Large V_{rms} = \frac{V_{max}}{\sqrt{2}}

Тогда мощность рассеиваемая на резисторе:

\Large P_{r} = \frac{I^{2}R}{2}

Энергия накапливаемая в индуктивности:

\Large W_{L}= \frac{LI_{rms}^{2}}{4}

Энергия накапливаемая в конденсаторе, но выразив через ток:

\Large W_{C}= \frac{CU_{rms}^{2}}{2} = \frac{I_{rms}^{2}}{4\cdot Cw^{2} }

Вернёмся к выражению (3) и запишем его оперируя мощностями и энергиями из уравнений выше.

\Large P = P_{r} + 2jw(P_{L}-P_{C}) (4)

Отсюда видно, что резонанс возникает когда накапливаемые энергии в конденсаторе и в индуктивности становятся равными. Или, если обратиться к уравнению (1), импеданс индуктивности становится равен импедансу конденсатора. Точка резонанса характерна минимальным входным сопротивлением (Z_in = R).

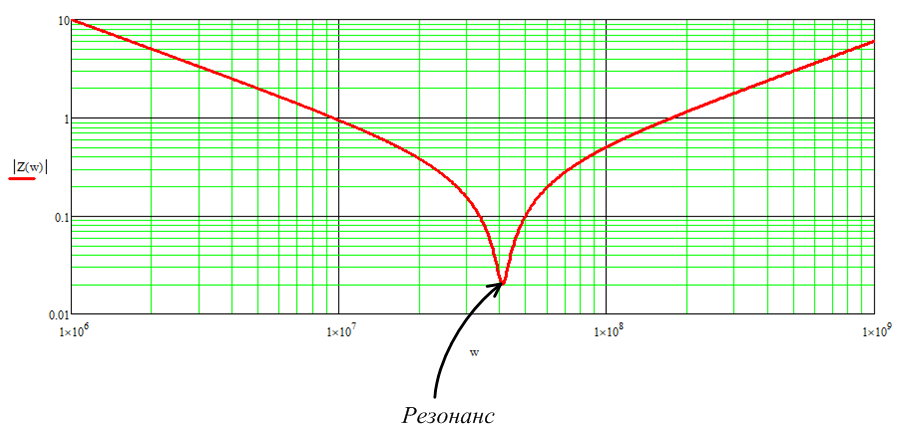
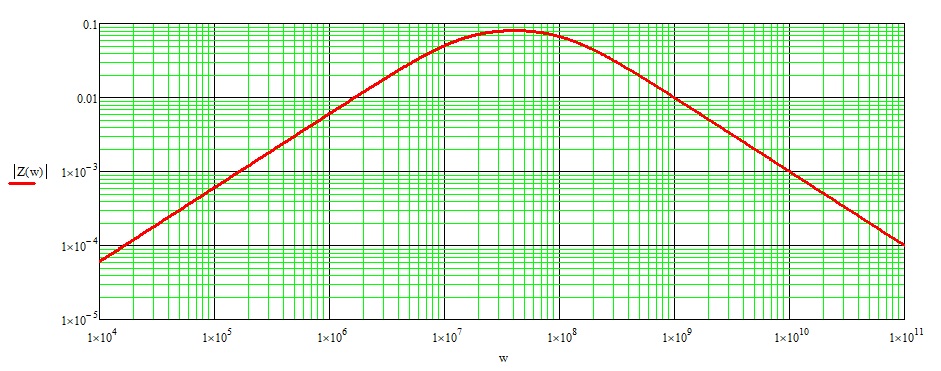
На графике импеданса, последовательный резонанс показан на рисунке ниже.

Как уже говорилось, условия для резонанса возникает когда WL=WC. Приравняем две энергии.

\Large \frac{LI_{rms}^{2}}{4} = \frac{I_{rms}^{2}}{4\cdot Cw^{2} }

Отсюда уже легко найти резонансную частоту.

\Large w_{0} = \frac{1}{\sqrt{LC}}

Далее найдём ещё один из важных параметров характеризующий резонансную цепь — это добротность. С помощью добротности часто описывают величину потерь в контуру. Так же с помощью добротности, можно определить насколько RLC цепь в целом подвержена колебаниям.

По сути добротность это — отношение запасаемой (хранящейся) энергии в цикле к энергии потерь. Обозначается как Q.

\Large Q_{0} =w_{0} \frac{W_{stor}}{W_{loss}} = w_{0} \frac{W_{L}+W_{C}}{W_{loss}} (5)

Давайте далее рассмотрим формулу для добротности для резонансной частоты w0. Как уже писалось выше, на частоте резонанса энергия в конденсаторе и в индуктивности равны. Учтём это в формуле (5).

\Large Q_{0} =w_{0} \frac{2W_{L}}{W_{R}} = w_{0} \frac{2\cdot \frac{I^{2}L}{4}}{\frac{I^{2}R}{2}} = w_{0} \frac{L}{R}

То же самое можно расписать через энергию конденсатор.

\Large Q_{0} =\frac{1}{w_{0}RC}

И последнее, что стоит отметить для последовательного резонанса, это полоса пропускания резонанса. Что это такое? На словах это можно описать так: полоса пропускания для резонансной цепи- это область частот, которая лежит внутри границ, где мощность рассеиваемая резистором меньше половины всей мощности системы. Найти ширину полосы можно вот так:

\Large BW = w_{0} \frac{1}{Q_{0}}

Границы полосы можно найти простым способом, например от частоты w0 отступить в каждую сторону по BW/2. Так же это можно сделать через передаточную функцию для RLC цепи по отношению к резистору. Запишем передаточную функцию как отношение Vr/Vin.

\Large \frac{V_{r}}{V_{in}} = \frac{IR}{I(R+jwL+\frac{1}{jwC})} = \frac{R}{R+\frac{(jw)^{2}LC+1}{jwC}}

Далее каждый член уравнения умножаем на jwC/jwC

\Large \frac{V_{r}}{V_{in}} = \frac{jwRC}{jwRC-w^{2}LC+1}

Теперь находим модуль передаточной функции. Напомню, что модуль для комплексных чисел находится как:

\Large \sqrt{(RE)^{2}+(IM)^{2}}

Теперь запишем окончательный вариант модуля передаточной функции.

\Large \left | \frac{V_{r}}{V_{in}} \right | = \frac{wRC}{\sqrt{(wRC)^{2}+(1- w^{2}LC)^{2}}} (6)

После того как мы записали передаточную функцию вернёмся к определению полосы пропускания. Полоса пропускания для резонансной цепи- это область частот, которая лежит внутри границ, где мощность рассеиваемая резистором меньше половины всей мощности системы.

Другими словами, чтобы найти полосу пропускания необходимо задаться условиями, где на резисторе будет рассеиваться половина всей мощности. Для этого амплитуда на резисторе должно быть равна как минимум:

\Large \frac{1}{\sqrt{2}}V_{max}

Зная эти условия, вернёмся к уравнению с учётом вышесказанного (6).

\Large \frac{1}{\sqrt{2}} = \frac{wRC}{\sqrt{(wRC)^{2}+(1- w^{2}LC)^{2}}} (7)

Теперь мы можем решить уравнение (7) относительно w. После решения получаем следующие корни:

\Large w_{1,2} = (\sqrt{1+(\frac{R}{2\sqrt{\frac{L}{C}}})^{2}} \pm \frac{R}{2\sqrt{\frac{L}{C}}})_{w0}

Выделим полученные частоты на графике импеданса, который фигурировал выше.

Параметры для построения.

Параллельный резонанс RLC

Опишем всё тоже самое, что выводили для последовательного RLC резонанса, но в более сжатой форме.

Выражение для импеданса Z_in:

\Large Z_{in} = (\frac{1}{R}+\frac{1}{jwL}+jwC)^{-1}

График зависимости импеданса от частоты:

Резонансная частота находится так же как и для последовательного резонанса и равна:

\Large w_{0} = \frac{1}{\sqrt{LC}}

Добротность для параллельного резонансного контура:

\Large Q_{0} = \frac{R}{w_{0}L} = w_{0}RC

Ширина полосы пропускания, также как и в последовательном RLC контуре, за исключением, что добротность должна быть для параллельного RLC контура.

\Large BW = w_{0} \frac{1}{Q_{0}}

Вывод или на что необходимо обратить особое внимание.

Часть того, что тут описано, наверное, интересно в первую очередь с академической точки зрения, но я считаю, иногда необходимо пройтись по базовым вещам и понимать откуда берутся те или иные формулы, которыми мы пользуемся при разработке.

Отдельно хочу обратить внимание на то, как ведёт себя график импеданса в зависимости от частоты. Такие зависимости импеданса очень часто применяются при построении схем. Также очень полезно понимать поведение импеданса в резонансных цепях для анализа целостности питания(PDN).

Также пара слов про добротность. В значение добротности есть три важных порога.

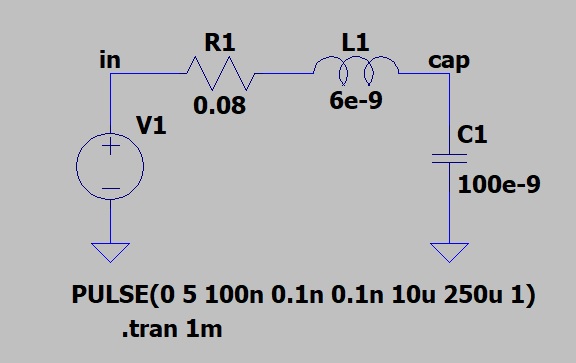
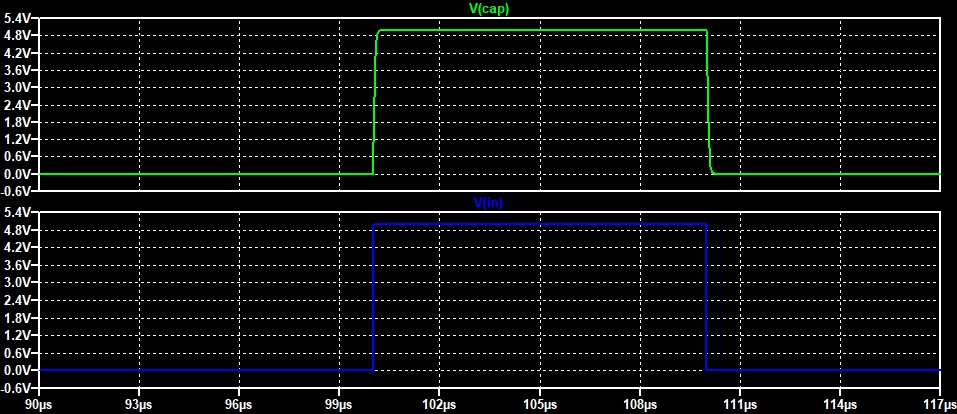
Q > 0.5 . В схеме с такой добротностью возникают колебания. Чем больше добротность, тем сильнее и дольше будут колебания. Ниже приведён пример подачи ступенчатого импульса, на последовательную RLC цепь. Добротность схемы Q0 = 3.

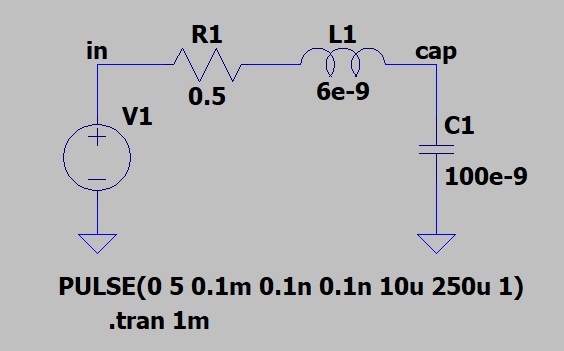
Q < 0.5 . В схеме с такой добротностью не возникают колебания.

Q = 0.5. Тут обойдёмся без схем и осциллограмм. Также как и для Q < 0.5 не возникает колебаний. Но значение равное 0.5 является наиболее оптимальным с точки зрения скорости нарастания сигнала и при этом выбросы или колебания сигнала не возникают. Все схемы где Q > 0.5 дают выигрыш для скорости нарастания, но в замен мы расплачиваемся колебательным процессом и выбросом напряжения (смотри осциллограмму для Q > 0.5).