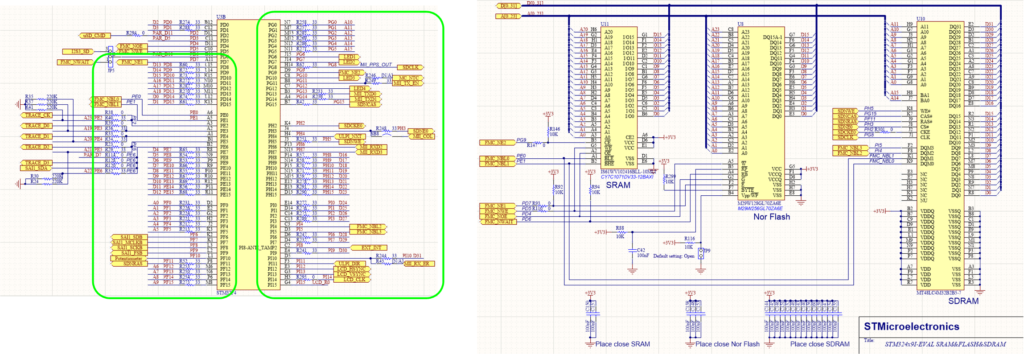
Если открыть reference design с простенькой памятью SDRAM и микроконтроллером, часто можно встретить, что на шине данных и шине адреса стоят последовательные резисторы 33 Ом. Например так сделано в reference design STM32439I-EVAL.
Разберёмся зачем они здесь!
Восстановление схемы.
Для начала полностью восстановим схему. Начнём с схемы которая представлена в reference design, затем постепенно будем погружаться глубже в детали.
Для наглядности упростим схему до уровня блочных соединений.

Теперь давайте разберёмся, что из себя представляет GPIO. По сути мы знаем, что при инициализации FMC контроллера в STM32 выводы GPIO настраиваются как push-pull каскад, в случае проходит цикл записи.
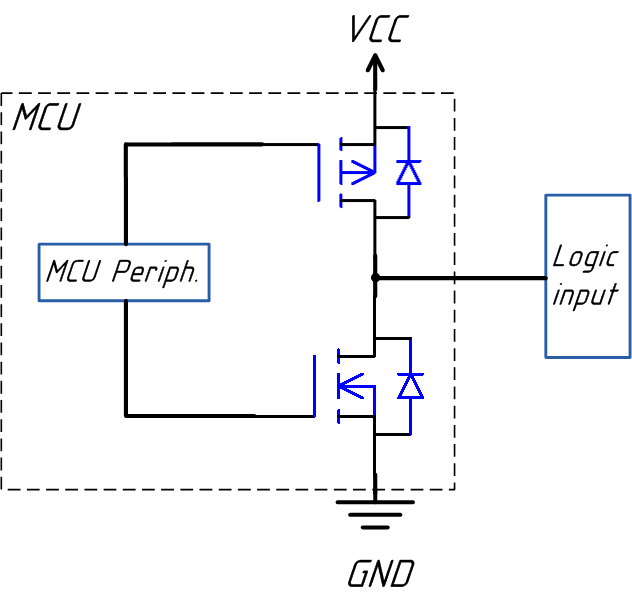
Push-pull выход можно представить как эквивалентный источник напряжения, с выходным сопротивление R.
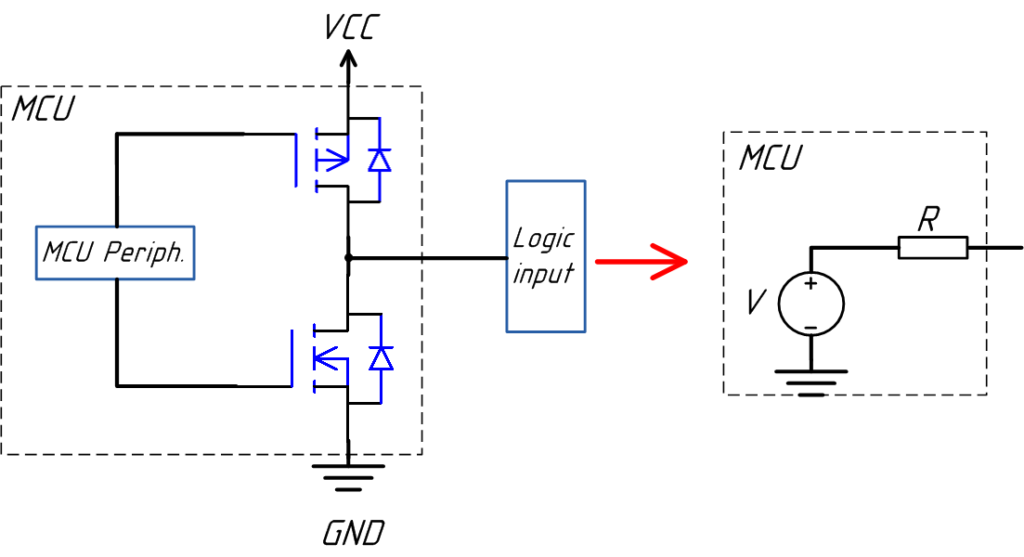
Для уточнения модели необходимо найти сопротивление R. Данное сопротивление можно найти по косвенным параметрам из datasheet на микроконтроллер. Для примера откроем datasheet на STM32F437. Открываем таблицу 57. Обращаем внимание на «Output low level voltage for an I/O pin».
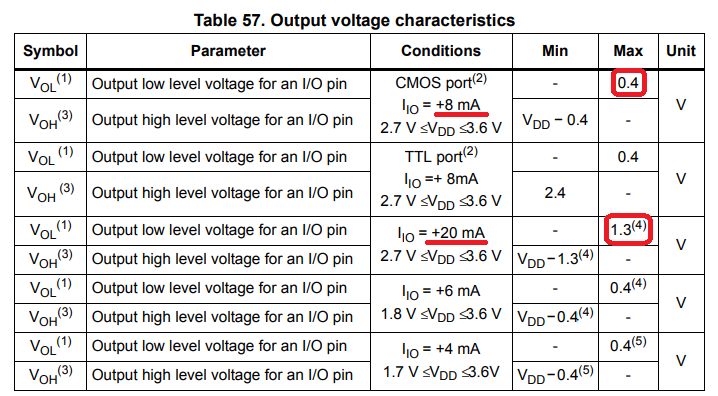
В таблице показывается, что если при логическом нуле на выходе GPIO, в порт втекает ток 20мА, напряжение на выходе не должно превышать 1.3В. Применив закон Ома, можно сказать о приблизительном сопротивление канала открытого транзистора в push-pull каскаде. Или переводя в эквивалентную схему, то выходном сопротивление эквивалентного источника питания.
Находим сопротивление:
R = \frac{V_{OL}} {I_{IO}} = \frac{1.3V} {20mA} = 65\Omega
Получилось 65 Ом, в реальности оно будет меньше. Т.к. расчёт производился для максимальных значений напряжения Vol. Для построения более точной модели, хотелось бы иметь типовые значения сопротивления, а так же другие паразитные параметры
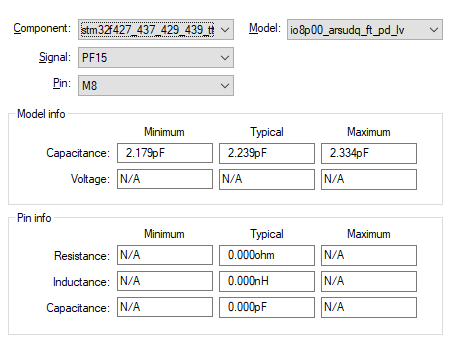
В этом нам поможет IBIS модель. Чтобы иметь представление что это такое можно почитать вот тут — link. Скачав модель интересующей нас микросхемы, смотрим на её содержимое. Например нас интересует порт PF15.
IBIS модель в себе содержит табличную информацию ВАХ характеристики о каждом порте GPIO + информация о портах питания для PDN анализа. Информация о GPIO содержится в виде табличной ВАХ, которая построена для диапазона от -Vpower до +2*Vpower.
Небольшое отступление касаемо момента, почему же от -3.3V до +6.6V?
Всё дело в том, что ibis модели были специально созданы для моделирование высокочастотных цепей, как правило на высоких частотах цепь рассматривают как длинную линию. В длинных линиях есть такое понятие как отражение сигнала, так вот если нагрузка на конце линии полностью разсогласована с импедансом линии/источника сигнала, возникает полное отражение. При полном отражение, обратная волна отражается с той же амплитудой что и исходный сигнал. В итоге на входе микросхемы кратковременно становится двойное напряжение, или 6.6V. Чтобы САПР мог адекватно смоделировать полное отражение сигнала, стандарт ibis требует наличия ВАХ для диапазона -Vpower : +2Vpower.
Так же ibis модель содержит информацию о паразитных параметрах вносимые корпусом. На картинке выше, они нулевые т.к. для частот на которых работает микросхема, они не существенны.
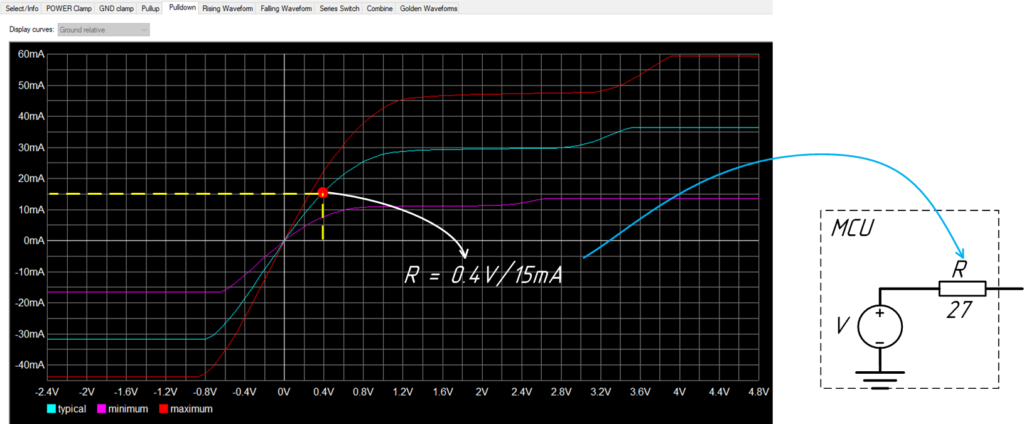
Ещё есть информация о паразитной ёмкости драйвера, он нам ещё пригодится. А пока что построим график ВАХ в графическом виде.
Из диаграмм ВАХ, можем получить типовое сопротивление для моделирования с эквивалентным источником напряжения.
Также учтём описанную в модели ёмкость в 2.24pF. В конечном итоге получаем вот такую схему GPIO:
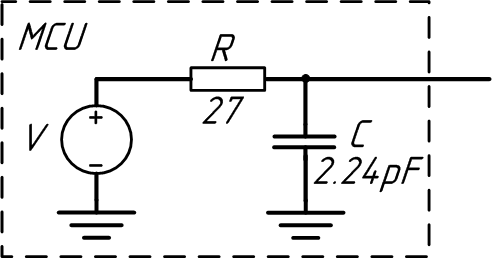
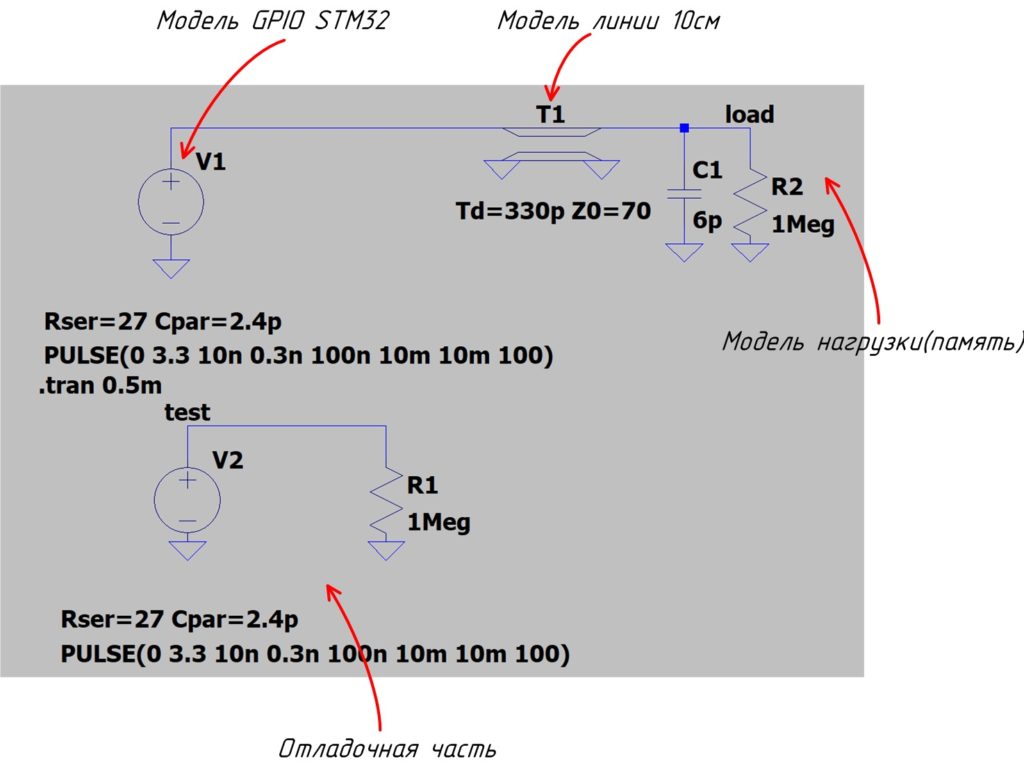
Дополним нашу упрощённую схему нагрузкой.
В схеме С_load это суммарная входная ёмкость микросхем.
R_ser последовательный резистор 33 Ом.
А так же линия передачи(дорожка на плате), которую будем рассматривать как линию с распределёнными параметрами или как с сосредоточенными.
Если формулировка распределёнными/сосредоточенными параметрами непонятно, необходимо хотя бы в бегло изучить тему длинных линий(например тут: раз, два).
Далее мы будем рассматривать схему из рисунка выше, меня номиналы компонентов и параметры линии. Анализ будет проводится в LTSPICE.
Анализ схемы
Для начала определимся когда будем использовать линию с распределёнными параметрами, а когда с сосредоточенными.
Сосредоточенные или распределённые?
Для того чтобы убедиться, что перед нами линия с распределёнными параметрами достаточно соответствовать эмпирическому правилу:
{\LARGE \frac {1}{4} \lambda > \textrm{Length trace}}
где \lambda — длина волны сигнала которую можно найти как: {\LARGE \frac {v}{f}} , f — частота сигнала, v — скорость распространения сигнала по плате. Чтобы примерно ориентироваться можно воспользоваться табличкой с сайта Henry Ott. Используя таблицу необходимо учитывать, что приведённые значения соответствия длины волны и длины трассы на печатной плате приведены для скорости света, в реальности же скорость распространения сигнала ниже и зависит от применяемого материала.
Написанное выше справедливо для синусоидального сигнала. Но например спектр из меандра 1MHz состоит из множества синусоид(см. главу импульсное потребление). В данном случае для оценки линии передачи необходимо знать время нарастания/спада сигнала и воспользоваться следующим уравнение:
{\LARGE f = \frac {0.35}{t_r}} , тут в знаменатели время нарастания. После того как найдём частоту возвращаемся к предыдущему абзацу.
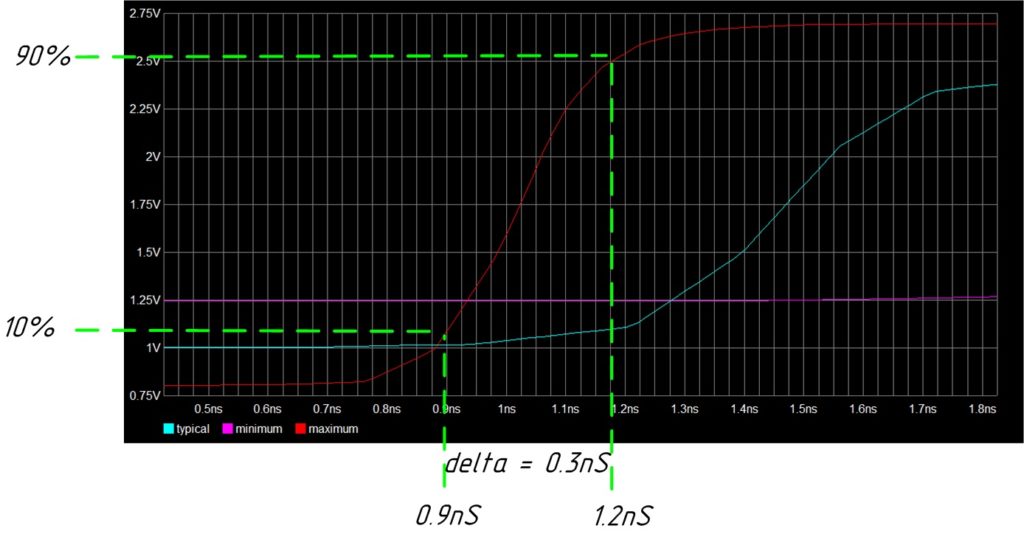
Для нашего примера информацию о времени нарастания возьмём всё из той же ibis модели.
Подставляем цифры и получаем {\large f = 1.2 \cdot 10^9 Hz}
Теперь находим длину волны для заданной частоты. Скорость распространения найдём из формулы: {\large v = \frac{c}{\sqrt{Er}} = \frac{3\cdot 10^8}{\sqrt{4}} = 1.5 \cdot 10^8} . Находим длину волны{\large \lambda = \frac{1}{2}\cdot\frac{1.5\cdot 10^8}{1.2 \cdot 10^9} = 6.2cm } .
Тут стоит отметить, что длина получена для частоты 1.2 ГГц. Если представить сигнал как множество синусов разной частоты, 1.2 ГГц это самый высокочастотный синус из всего множества для рассматриваемого сигнала, и при этом он несёт в себе меньше всего энергии. Поэтому, если для этой частоты возникает отражения , то это не слишком сильно влияет на целостность сигнала. Именно поэтому мы немного отступили от эмпирического правила в формуле и вместо 1/4 взяли 1/2.
Что имеем в итоге! Если длина дорожки на плате больше чем 6.2cm, то необходимо линию рассматривать как длинную(распределённые параметры). Если же меньше чем 6.2cm, тогда рассматриваем как линия с сосредоточенными параметрами. Далее рассмотрим оба случая.
Длинная линия.
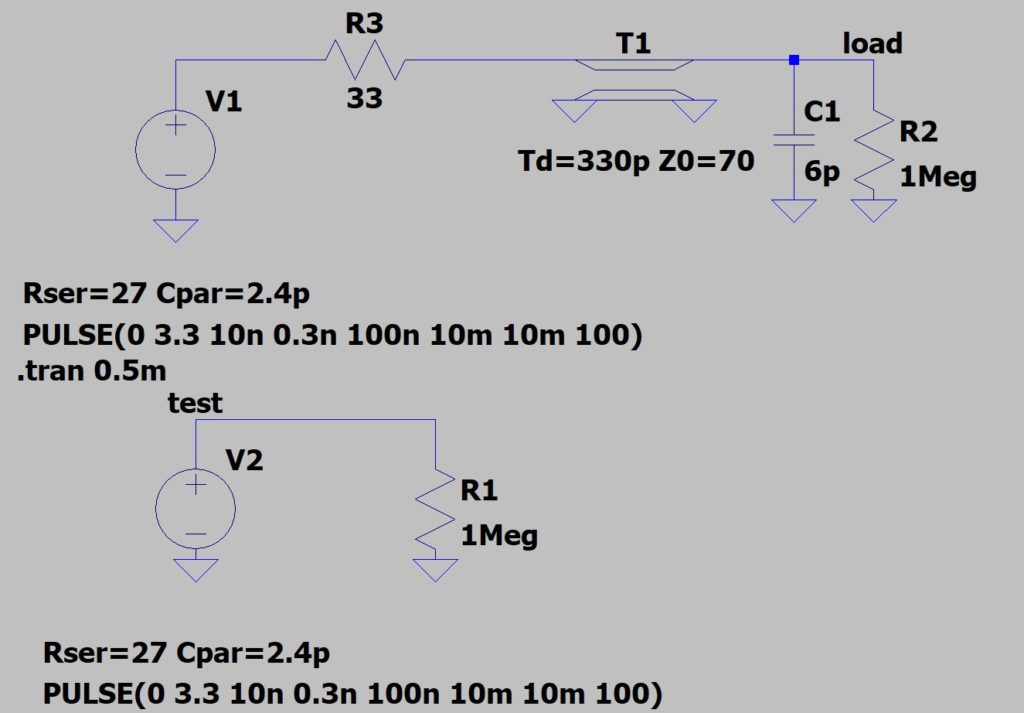
Смоделируем влияние добавочного резистора в цифровой линии длиной 10cm. Для моделирования воспользоватся программой LTSPICE.
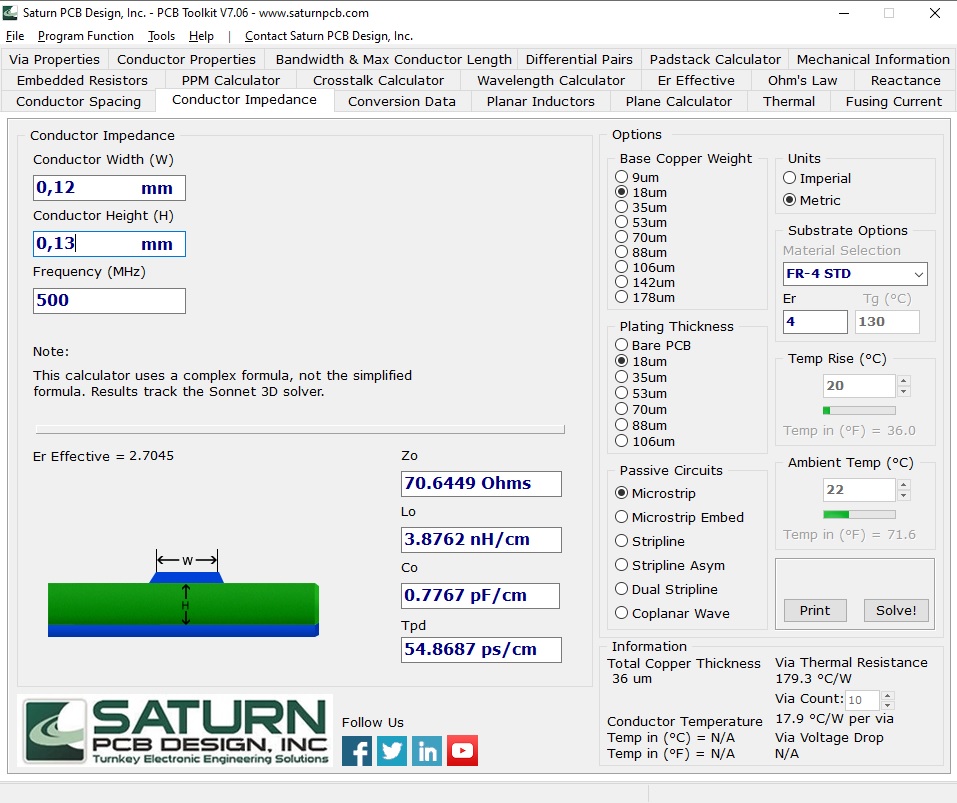
Td = 330p это время линии задержки длиной 10см(LTSPICE считает, что сигнал распространяется с скоростью света). Z0 = 70, это типичное сопротивление для дорожки с параметрами как на рисунке ниже.
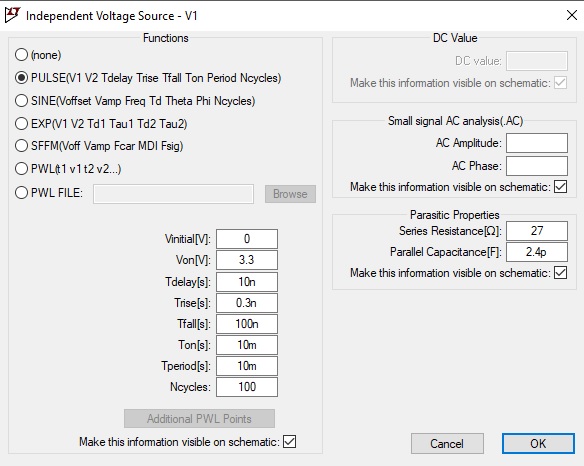
Источник напряжения настроен следующим образом:
Для начала промоделируем схему, с отсутствующим последовательным резистором.
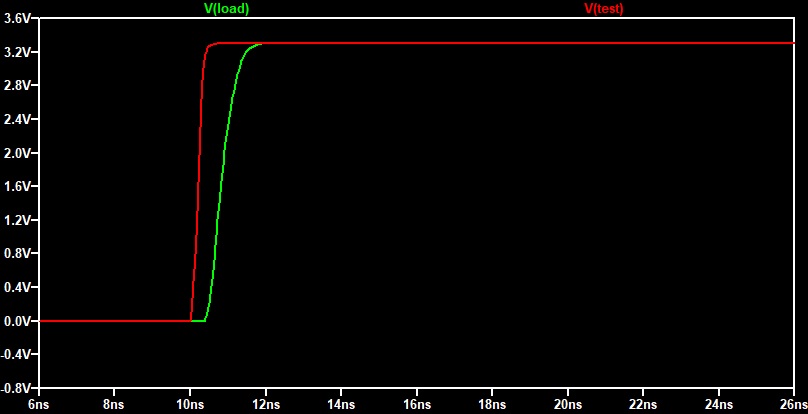
Как мы видим из за несогласованности линии происходит многократное отражение сигнала, и наблюдается перенапряжение до 4.5V. В реальности перенапряжение будет меньше за счёт clamp diode в цифровых микросхемах, но тем не менее неприятности остаются.
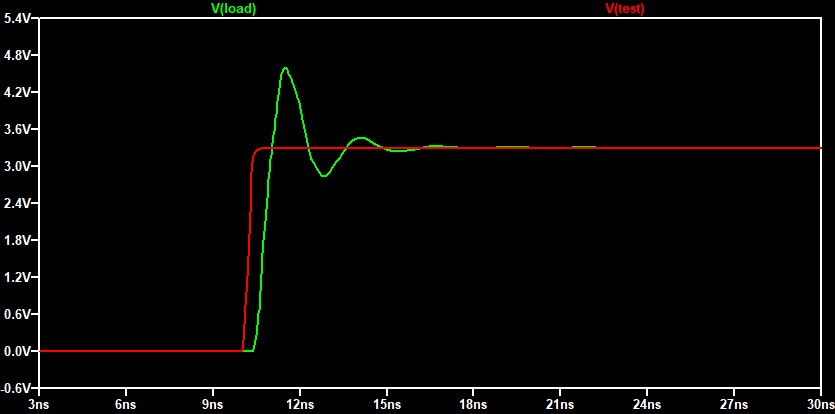
Теперь изменим нашу модель, добавив резистор 33 Ом, и промоделируем заново.
За счёт того, что появился добавочный резистор R3 = 33 Ом, отражение стало незначительным и исчезли выбросы напряжения на нагрузки. Так же стоит отметить, что изменился dv/dt в меньшую сторону, что немного улучшает эмиссию.
Сосредоточенные параметры
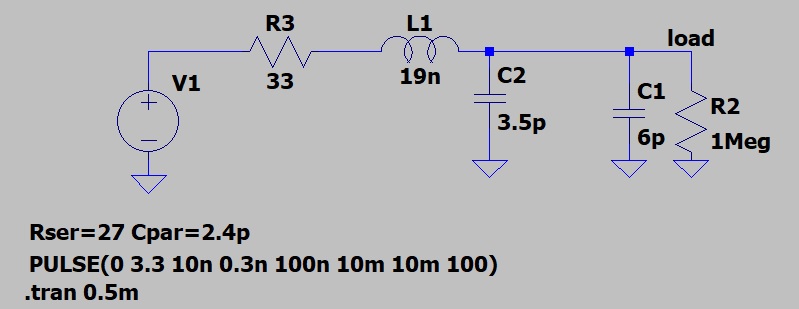
Пусть максимальная длина дорожки равна 5cm. Зная погонную индуктивность и ёмкость(из рисунка » Параметры линии.»), заменим дорожку на LC элемент.
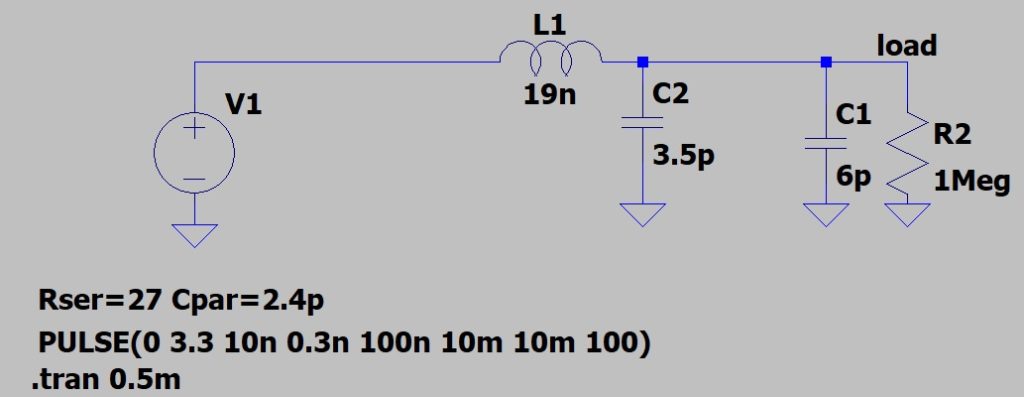
Параметры источника питания остаются как в модели с длинной линией. Посмотрим напряжение на нагрузке.
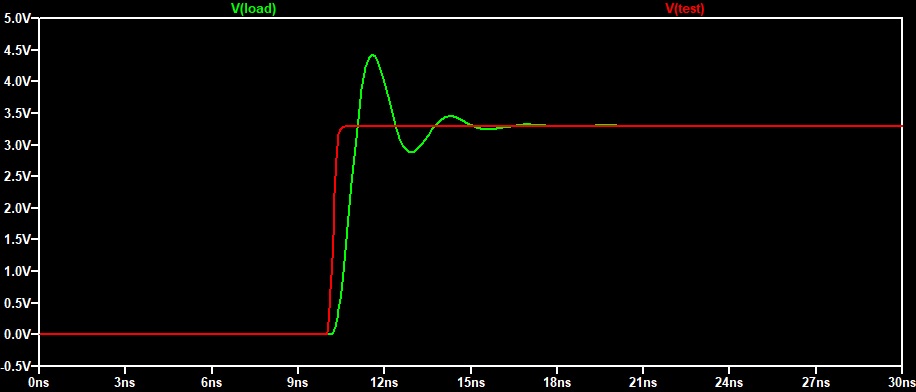
В данной модели выброс напряжения вызван резонансным процессом. Так как. индуктивность гораздо больше ёмкости, добротность(Q) >0.5, следовательно наблюдается резонанс. Чтобы избежать резонанса, можно увеличить ёмкость. Но данный подход не применяется, поскольку добавив ёмкость, мы нагружаем выходной драйвер микросхемы. Поэтому добавим резистор 33 Ом как в схеме и посмотрим, что будет.
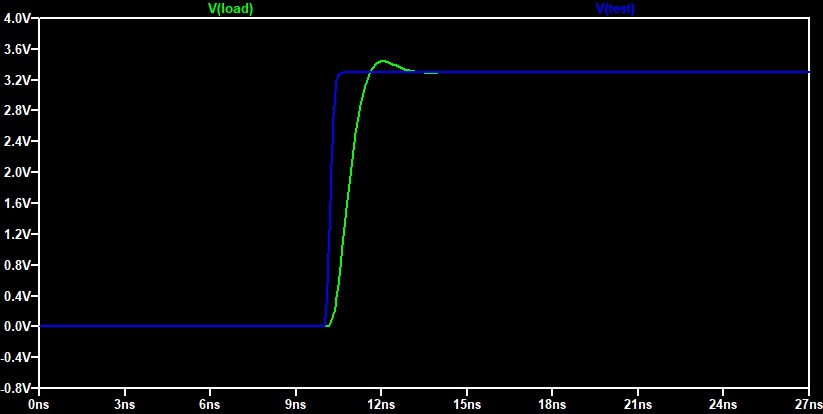
После добавления резистора, добротность в цепи уменьшилась. Как следствие уменьшение добротности, исчез большой выброс напряжения.
Вывод
Для цифровых интерфейсов, у которых нет требований к волновому сопротивлению иногда добавляют последовательный резистор, дабы улучшить целостность цифрового сигнала.
Даже если линия не является длинной, не стоит забывать, что цифровой вход имеет достаточно низкую входную ёмкость и при достаточно небольшой индуктивности дорожки получается последовательный резонансный контур с Q > 0.5. Добавочный резистор, эффективный метод снизить добротность, при этом сильно не ухудшив скорость нарастания.