Применение ферритовых бусинок

В этой статье (или даже небольшом цикле статей) я бы хотел коснуться нескольких вопросов построения фильтров с применением ферритовых бусинок(ferrite bead). Для начала сформулируем список вопросов, на которые постараемся дать ответы:

1. Ферритовая бусинка и индуктивность, в чём разница?
2. Как правильно применять ферритовые бусины?
3. Можно ли навредить применяя ферритовую бусину?

Немного о физике магнитных процессов.

Начнём из далека и поговорим о физике в ферритах и немного о природе магнетизма.

Вообще наиболее близко к пониманию магнетизма приблизились в 1819-1820 годах когда обнаружили, что магнитное поле образуется в проводнике с током. Затем сразу же обнаружили, что провода, по которым протекает ток, притягиваются друг к другу или отталкиваются, в зависимости от направления тока.

Вообще наиболее близко к пониманию магнетизма приблизились в 1819-1820 годах когда обнаружили, что магнитное поле образуется в проводнике с током. Затем сразу же обнаружили, что провода, по которым протекает ток, притягиваются друг к другу или отталкиваются, в зависимости от направления тока.

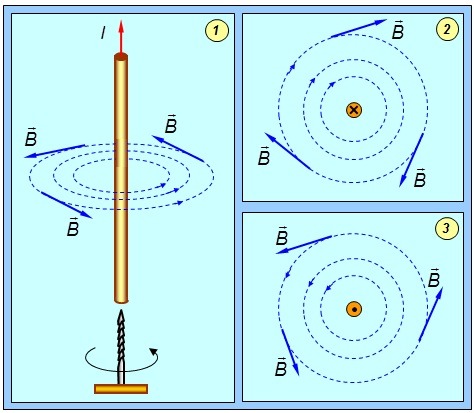
Если немного поразмыслить о том, что электрический ток это упорядоченное движение заряженных частиц и сопоставить этот факт с тем, что электрон вращается по орбите вокруг положительно заряженного ядра(по сути движение одной заряженной частицы), то можно говорить о существовании так называемого орбитального магнитного поля. В проводнике магнитное поле создаётся многочисленными движущимися частицами, а чем хуже одна частица которая движется вокруг ядра.

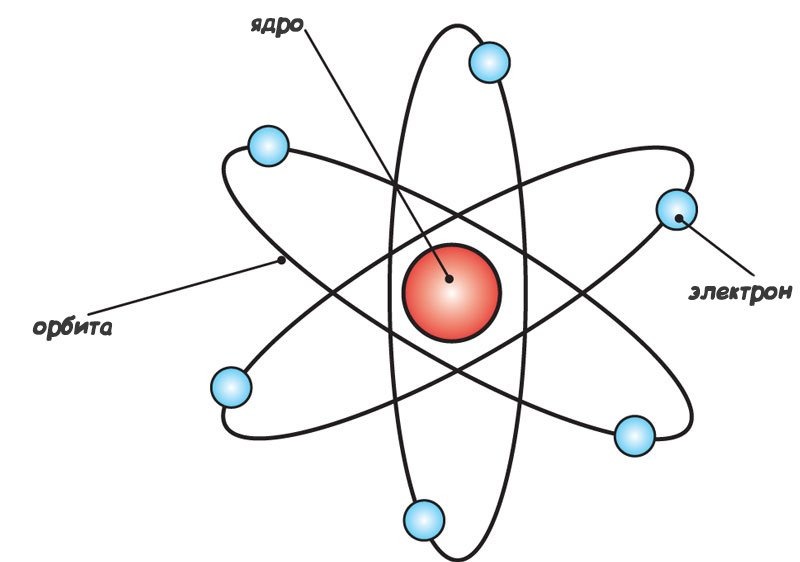
Но тут же можно закричать как в известном меме: NO GOD PLEASE NOOOO!!!

Всё дело в том, что современная теория устройства атома говорит от том, что нет никаких орбит и нам достоверно неизвестно вращается ли электрон по орбите, т.к. электрон это не частица в обычном понимании. Вместо орбит было бы правильно говорить про энергетические уровни, на которых вероятность «обнаружения» электрона высока. Для наглядности:

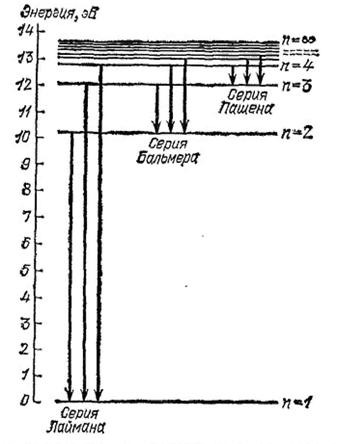
И если уж нам очень хочется представить движение электронов, то правильнее говорить про орбитали(НЕ орбиты). Представьте, что по закрашенным областям на картинке можно предсказать нахождение электрона с некоторой вероятностью, но определить точно где он находится невозможно. Сплошная неопределённость….

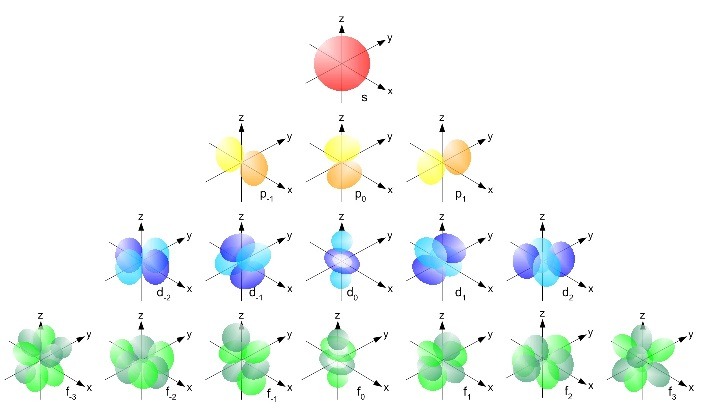
Вернёмся обратно к магнитному полю… Так называемая орбитальная составляющая магнитного поля нам не очень интересна, так как она помогает описать магнитное поле в средах которые называются диамагнетики и парамагнетики. А мы будем иметь дело с ферромагнетиками, именно с применением ферромагнетиков строится большинство индуктивностей и бусинок.

Магнетизм ферромагнетиков по большей части основывается на спиновом магнитном поле. Помимо вращения электрона относительно ядра, электрон вращается вокруг собственной оси, это явление называется спином.

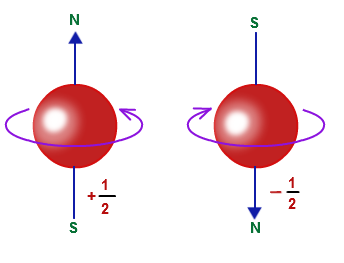
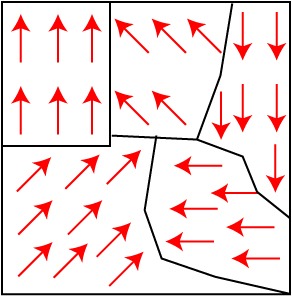
Расположение полюсов зависит от того, в какую сторону вращается электрон. Это означает, что электрон можно представить как маленький магнит с северным и южным полюсом. И как оказывается, в ферромагнетиках такие маленькие магнитики объединяются и образуют так называемые домены. Если рассмотреть ферромагнетик с точки зрения доменной структуры, то получится картина как на рисунке ниже.

А так это выглядит под микроскопом.

Из рисунка с красными стрелками видно, что границы имеют случайный характер, как и направления вектора магнитной индукции В(векторная величина, текстовый редактор не позволяет вставлять специальные символы прямо в текст, обозначающие вектор). Из-за случайности ориентации вектора В ферромагнетик не имеет собственного магнитного поля или оно очень мало. Но что происходит с доменами в внешнем магнитном поле? А вот что:

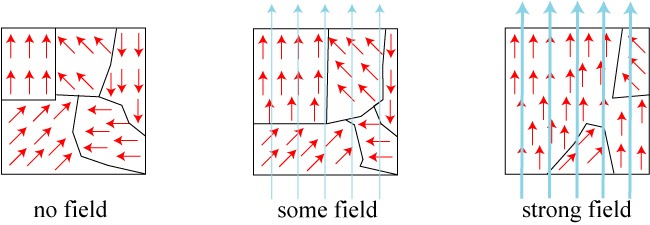
Чем сильнее магнитное поле, тем площадь доменных структур, которые сонаправлены с магнитным полем, становится больше. При очень сильном магнитном поле, в ферромагнетике практически не остаётся доменных структур которые направлены против вектора В. По сути самая правая картинка очень близка к насыщению ферромагнетика (сердечника в случае с индуктивностью/бусиной). Если теперь перейти к обычной индуктивности, то основной вклад в магнитную индукцию вносит поле созданное доменами, а внешнее поле вызывается протекающим током в проводнике, который намотан на сердечник. Мои слова неплохо демонстрирует рисунок ниже(не обращайте внимание на отсутствие сердечника на рисунке).

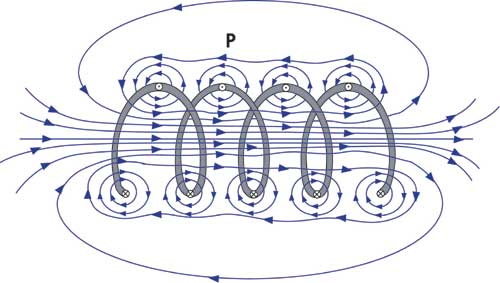
Всё это можно описать с помощью привычной нам петли гистерезиса.

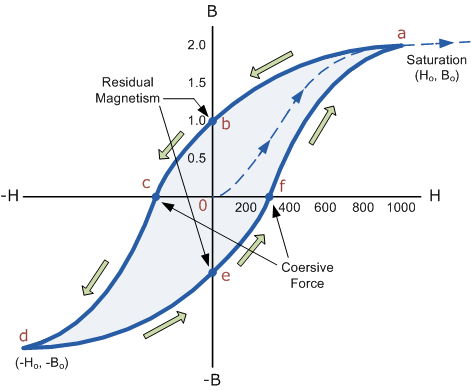
За магнитное поле, созданное проводом(без сердечника), отвечает вектор H. Результирующее магнитное поле — это вектор В. По петле гистерезиса очень просто понять процесс насыщения, мы увеличиваем Н, пропуская через провод больший ток, в свою очередь вектор В с определенного момента перестаёт увеличиваться, т.к. все домены уже ориентированы в одну сторону. И уже последующие увеличения Н не приводят к увеличению В. Таким образом, наша индуктивность превращается в обычный проводник. По сути это ответ на вопрос, что же случается с индуктивностью или трансформатором во время насыщения.

Связь между Н и В можно записать в следующим виде:

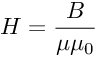
Движение доменных границ. Магнитная проницаемость.

Уже как было показано, под воздействием внешнего магнитного поля, границы доменов начинают увеличиваться или уменьшаться в зависимости от первоначального направления вектора В на участке домена. Если рассматривать общий случай с индуктивностью, то энергия, которую мы затрачиваем на перемагничивание(по сути энергия тратится на движение границ доменов), находится как:

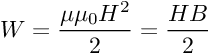
Но обращаю внимание, эта энергия которую мы затратили на перемагничивание, но это не значит, что мы её потеряли. Она накопилась, её значение так же можно определить в привычной нам форме.

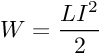
А что будет, если мы заставим двигаться доменные границы слишком быстро? В таком случае, привычные нам формулы энергии перестают быть точными и описание процессов в ферромагнетике становится возможным с помощью дифференциальных уравнений. В книге «Магнитные свойства аморфных и нанокристаллических сплавов»уравнение, описывающие движение магнитных доменов, записывается следующим образом:

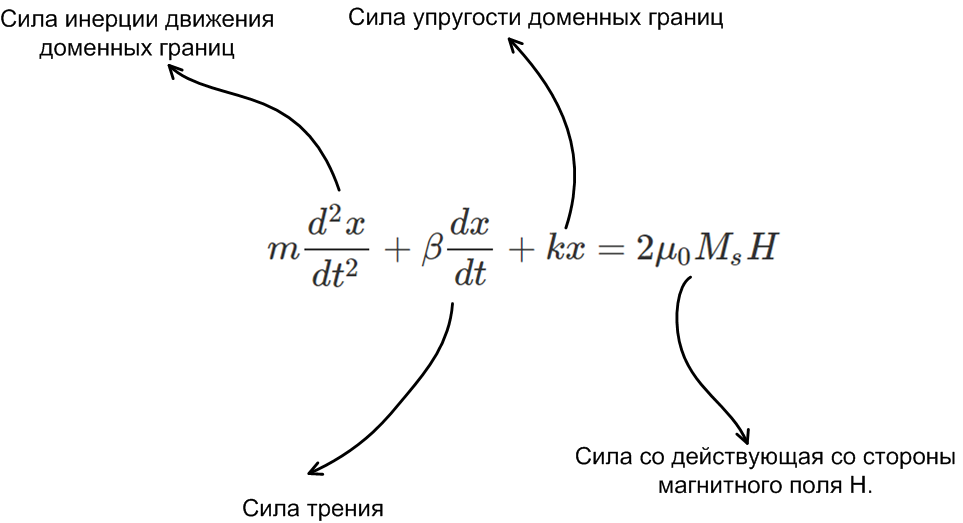
Коэффициенты в уравнении зависят от конкретного материала ферромагнетика.

Перейдя из механических сил к магнетизму, уравнение принимает вид:

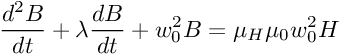
Если рассмотреть случай с синусоидальной значение Н и В. Окажется, что уравнение распадётся на две составляющие, с действительной частью Н и В и мнимой частью Н и В. Тогда, если говорить в контексте потерь в феррите, мнимая часть отвечает за потери.

По формуле выше видно, если Н и В мнимые, то и магнитная проницаемость μ так же может быть мнимой.

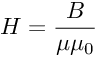
Типичная зависимость действительной и мнимой части μ от частоты выглядит как на графике ниже:

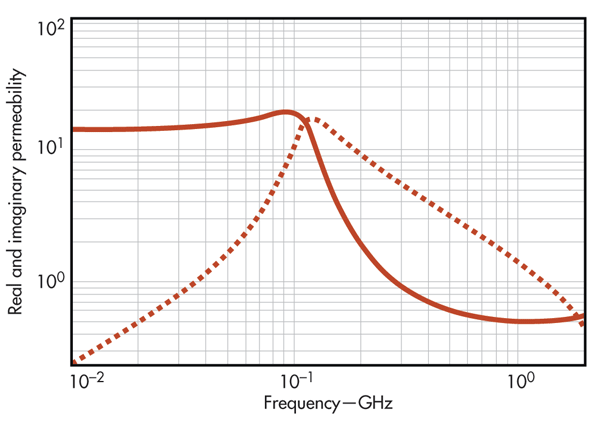
Если мнимая часть отвечает за потери, то с точки зрения ферритовой бусинки, необходимо её использовать для подавления той области частот, где мнимая μ» преобладает над действительной μ’.

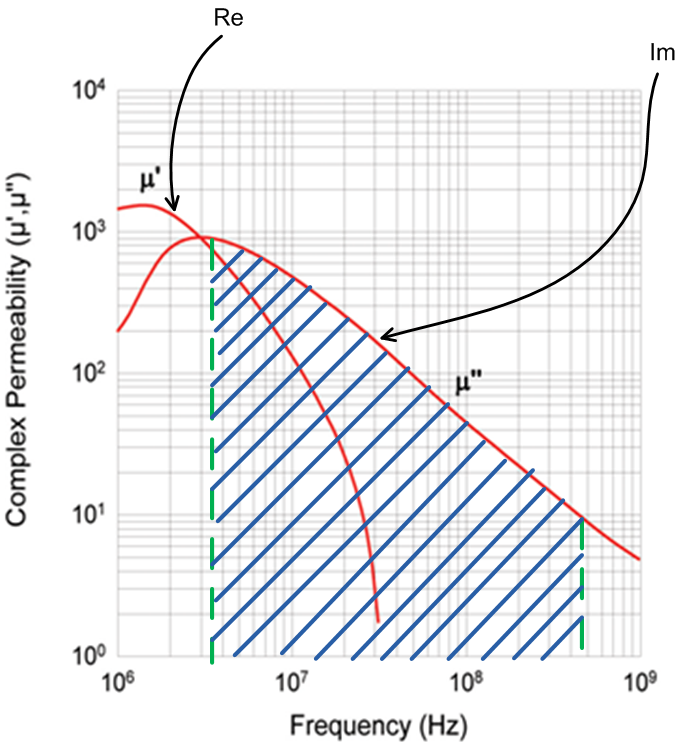
Если использовать ферритовую бусинку сделанную на материале с характеристиками как на рисунке выше, тогда данный компонент наиболее продуктивно применять для подавления помех в области частот которая закрашена синим цветом, в данной области частот помеха преобразуется в тепло. Забегая немного вперёд проведём следующую аналогию, когда энергия рассеивается в тепло, это эквивалентно активному сопротивлению. Так оно и есть, в синей области частот бусинка ведёт себя как обычное сопротивление. В области частот слева от синей части, как индуктивность.

Производители ферритовых бусинок редко приводят зависимости магнитной проницаемости(это больше прерогатива производителей сердечников) у себя в datasheet. Однако там можно найти зависимость импеданса от частоты, на примере datasheet компании Taiyo:

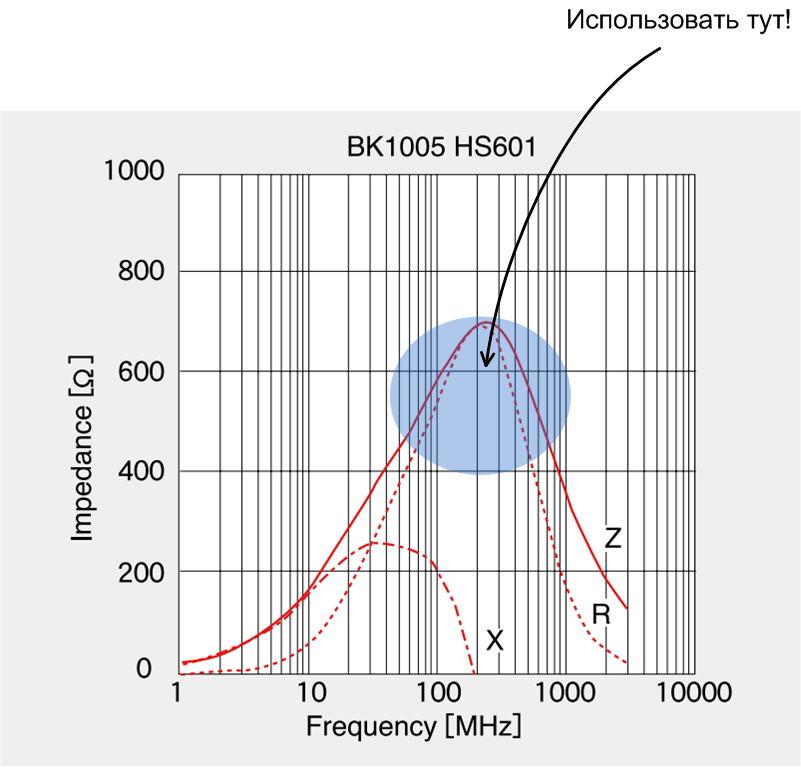
Из графика следует, что бусинка подходит для подавления частот от 100MHz до 500MHz.

Возможен ли такой же трюк с обычными индуктивностями на высоких частотах? В целом да, только есть большая разница в том какие сердечники используют для обычных индуктивностей и для бусинок. Как правило сердечники для бусинок делают специально с высокими потерями в области высоких частот, в свою очередь у сердечников для индуктивностей данные потери так же имеются, но они не настолько велики. Поэтому бусинки часто используют для подавления высокочастотных помех.

Определить источник помехи.

Перед тек как подойти к выбору ферритовой бусинки, необходимо определить, что защищаем и от чего защищаем. Часто на одном устройстве находится как и чувствительные цепи, так и источники помех. Например рассмотреть плату с микроконтроллером. Тогда основные помехи будут связанны с частотами тактирования или передачи данных. Вот так выглядит спектр EMI для 8bit PIC.

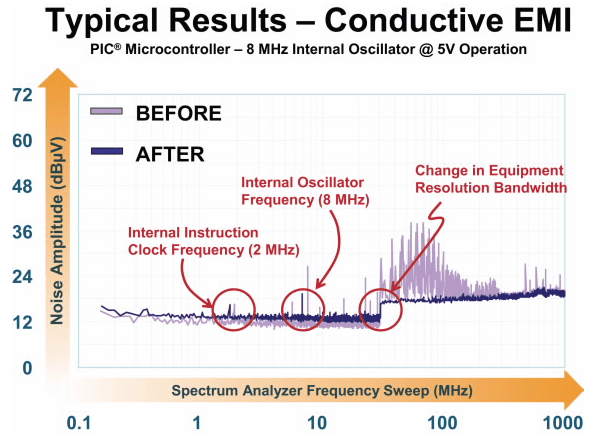
Не только, тактовые генераторы и цифровые линии передачи сигналов являются источниками помех. Например в этом спектре, проблемная частота оказалась 140MHz. Сначала можно подумать, что 140MHz является продуктом N-ой гармоники сигнала тактового сигнала. Но частота 140MHz не является нечётной гармоникой сигнала 10MHz. В конечном итоге, виновником была микросхема, которая потребляет импульсный ток на частоте 20MHz.

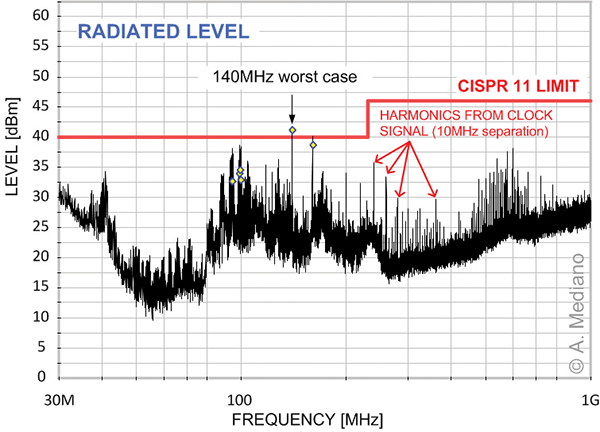
Как видно источником помех может являться почти любое электронное устройство или узел в вашей схеме. Но тем не менее, уже на этапе разработки схемы известны потенциальные источники помех, именно с ними и нужно бороться в первую очередь.

Применение бусинок для фильтрации цепей питания.

Если источник помехи находится на плате которую мы разрабатываем, то наилучшие место где необходимо ставить фильтр это вблизи источника помехи. В небольшом курсе от murata есть прекрасная иллюстрация которая демонстрирует, что будет если поставить фильтр вдали от источника помехи.

На рисунке показан провод, но вместо провода может быть та же дорожка на печатной плате. В противовес картинке выше, правильное расположение фильтра.

Та же ситуация, но при наличие экранирующего корпуса.

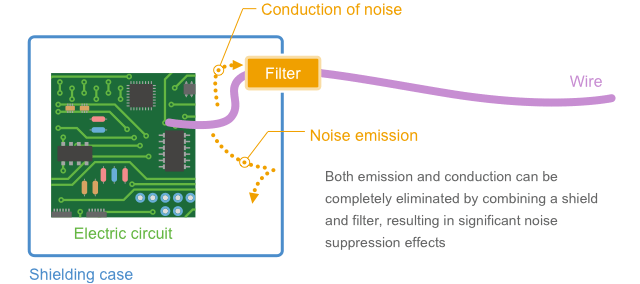
Пример реализации фильтра

Далее, чтобы не говорить об абстрактных помехах придумаем пример. Предположим вы разрабатываете устройство у которого на борту парочку USB HUB, к которым подключено несколько интерфейсных мостов.

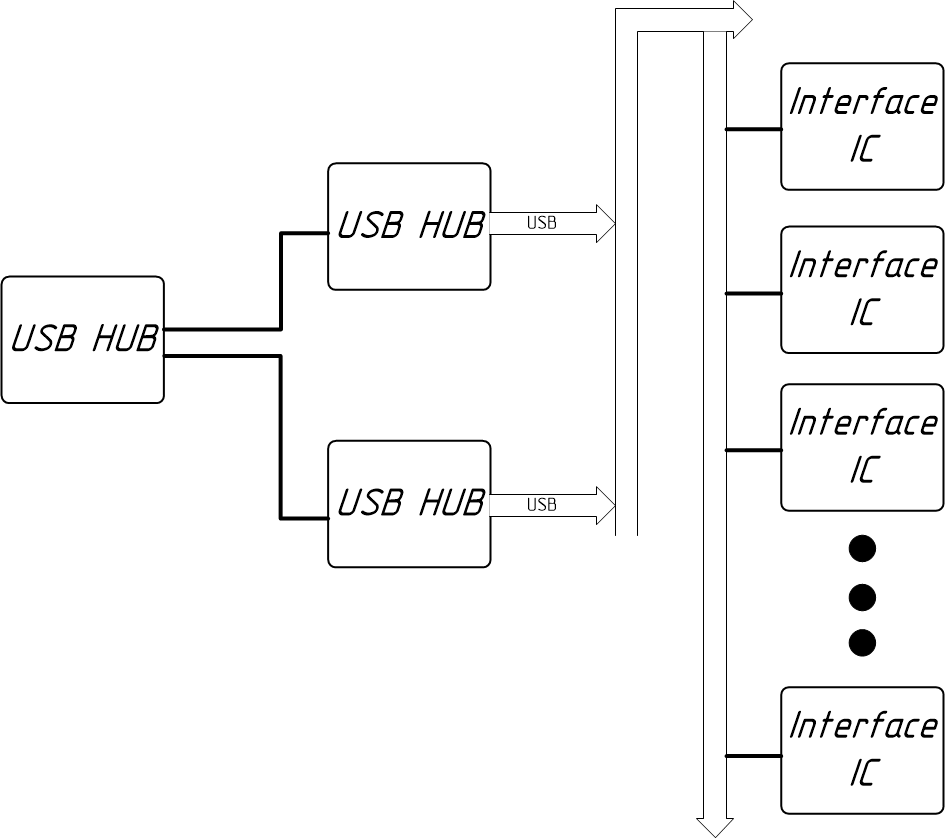
Каждый блочок нуждается в своём тактовом сигнале. Одним тактовым генератором не обойтись т.к. у выходного драйвера всегда есть ограничение по максимальной нагрузочной ёмкости.

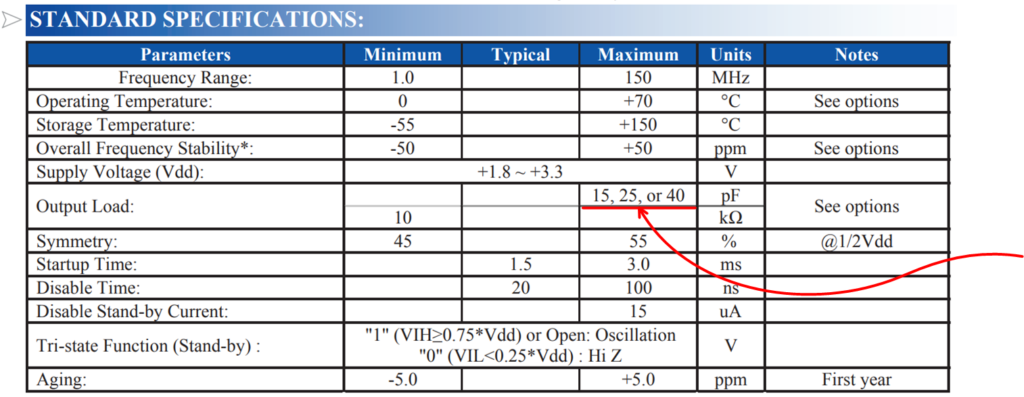
Ставить свой отдельный генератор/кварц становится не выгодно по себестоимости начиная с N штук(тут всё сильно зависит от параметров которые влияют на его цену).

Один из способов решения нашей задачи является применение так называемых Clock Buffer. Вот например один из представителей семейства CDCLVC1110PWR. На вход подаётся тактовый сигнал, на выходах он дублируется через буфер.

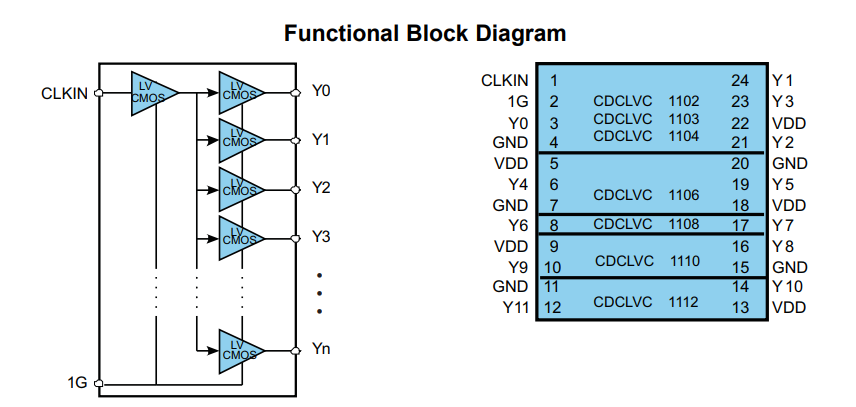
Пусть на CLKIN будет равен 48MHz, к выходам микросхемы подключены различные устройства, которые имеют паразитную емкость. На фронтах сигнала возникает импульсное потребление, контур перезаряда емкости проходит через цепь питания и развязывающие конденсаторы вблизи микросхемы.

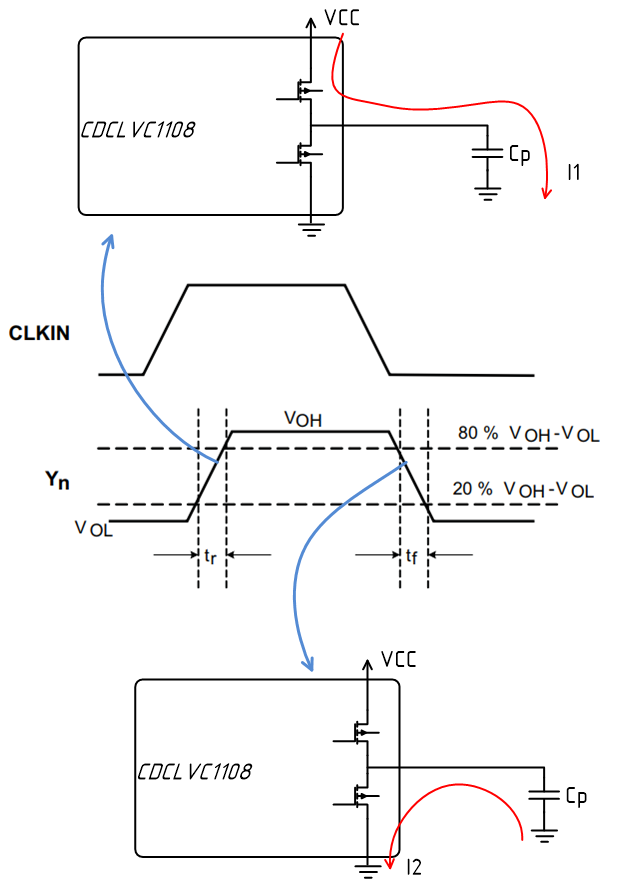
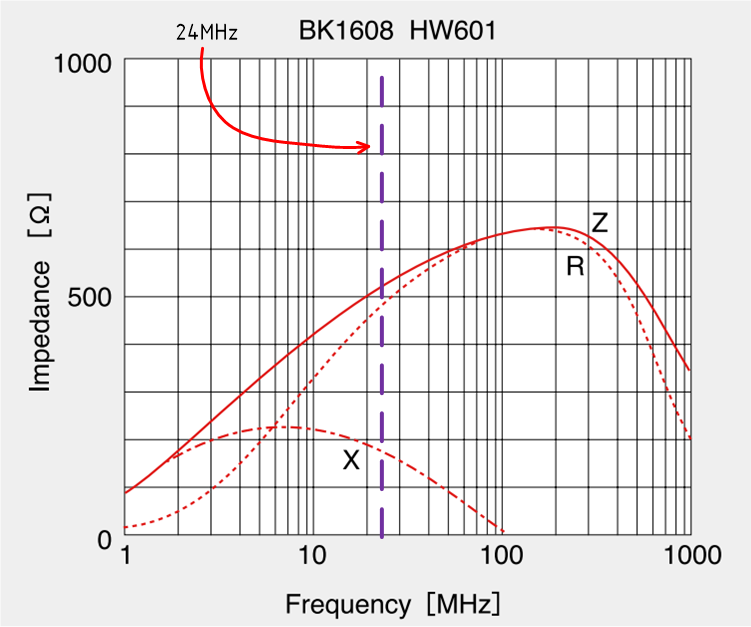
С точки зрения шины питания больше интересен верхний случай, т.к. контур лежит через шину питания. Зададимся частотой генератора = 24MHz. Под данную частоту неплохо подходит BK1608HW601.

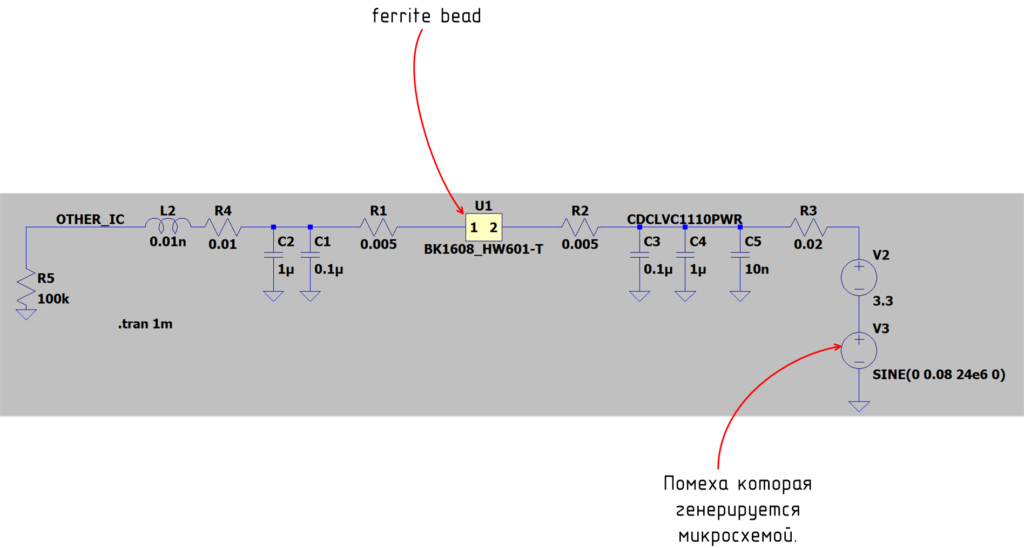
Создадим в LTSpice модель используемого фильтра для шины питания CDCLVC1110PWR с некоторыми паразитными параметрами(паразитные сопротивления показаны на схеме, ESL скрыто в параметрах конденсатора). В схеме есть серьёзное допущение. Оно заключается в представленной модели помехи. Модель самая простая — это синусоидальный сигнал амплитудой 80мВ частой 24MHz.

Ниже приведены результаты моделирования.

Напряжение питания + помеха от CDCLVC1108:

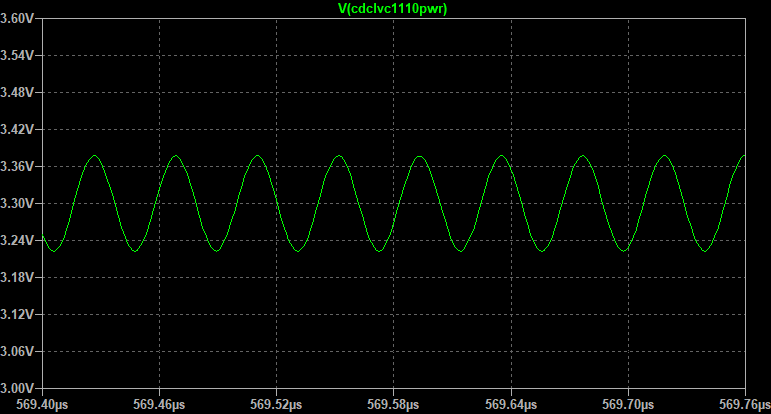
А вот что прошло к сигналу OTHER_IC:

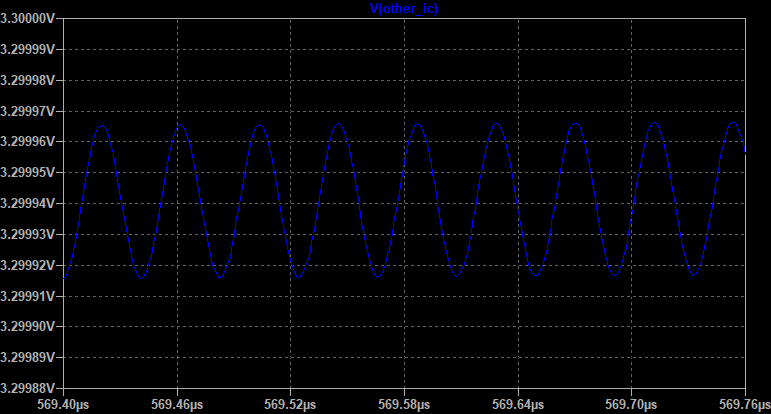
Для наглядности совместим две диаграммы:

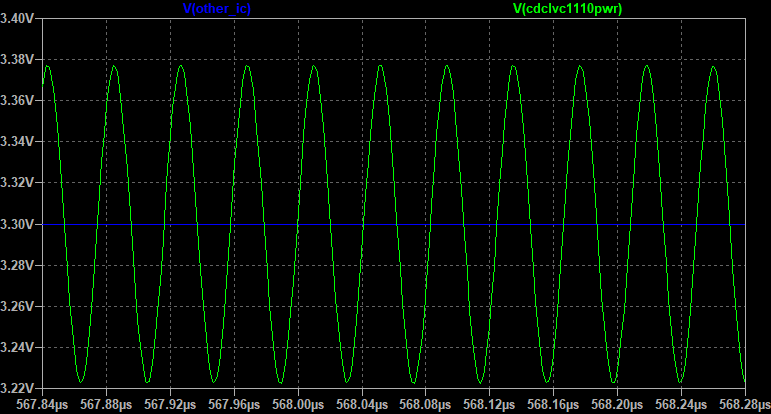
Результат ,как говорится, «на лицо». Почему так получилось можно объяснить достаточно просто. Сигнал питания можно разделить на две составляющие DC(V2 на модели) и AC(V3 на модели). Задача бусинки U1 создать невыгодный контур для протекания тока помехи. Что значит не выгодный? Как известно ток не дурак, и протекает по наименьшому сопротивлению. Наименьшее сопротивление в данном случае это импеданс C3||C4||C5.

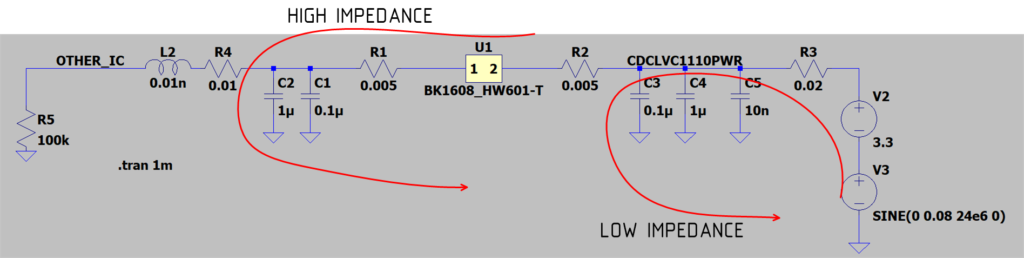
Как правило С3, С4 и С5 стоят вблизи ножки питания микросхемы. Тем самым контур получается коротким и дорожки/полигон не будет работать как антенна, излучая помеху.

Импульсное потребление.

Очевидно, что при импульсном выходном сигнале, потребление так же будет импульсное. Не смотря на то, что частота равна 24MHz, в спектре содержатся и другие частоты.

Например, спектр прямоугольного сигнала частотой 1MHz

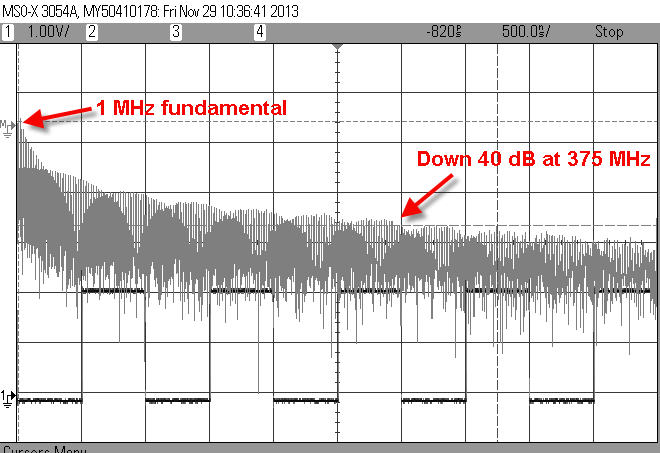
Поэтому рассматривать помеху как синусоиду одной частоты не совсем верно. Обновим нашу модель с учётом вышесказанного.

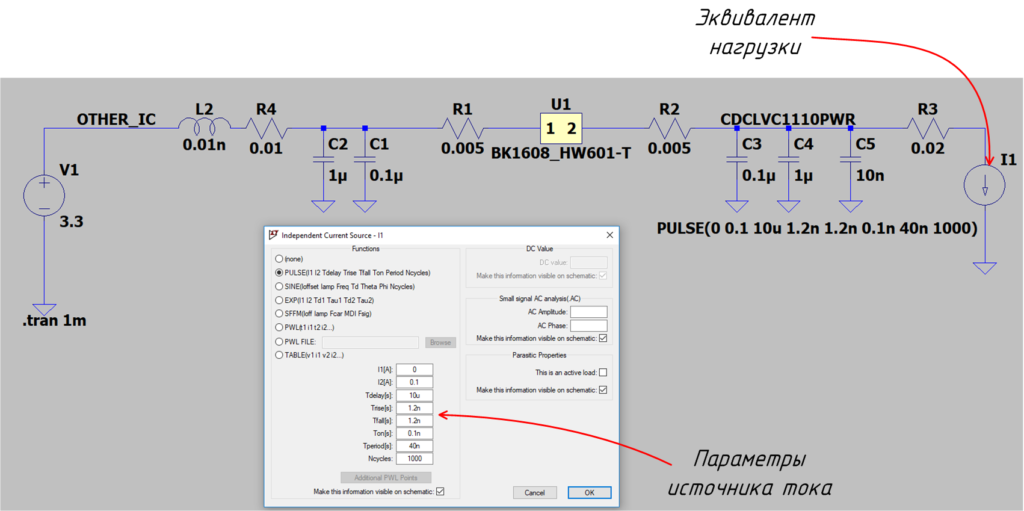
Посмотрим получившиеся диаграммы

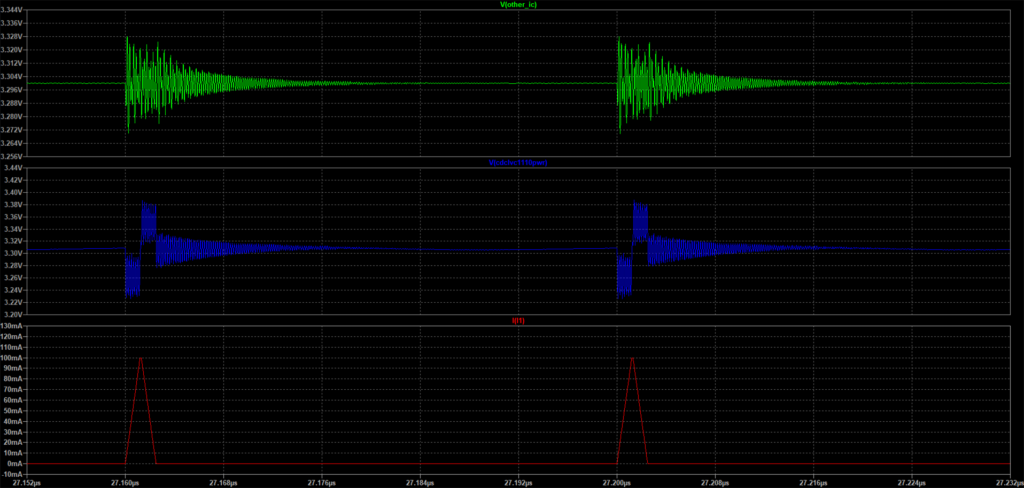
Даже с подходящей по частотным характеристикам ферритовой бусиной, возможны неприятные и длительные переходные процессы. Причина всему этому паразитный параметр конденсатора — ESL. Построение фильтров это комплексный подход. Важны параметры каждого компонента, и в данном случае, нельзя закрывать глаза на паразитные параметры тех компонентов, которые вы ставите.

Уменьшим значение ESL и сравним результаты.

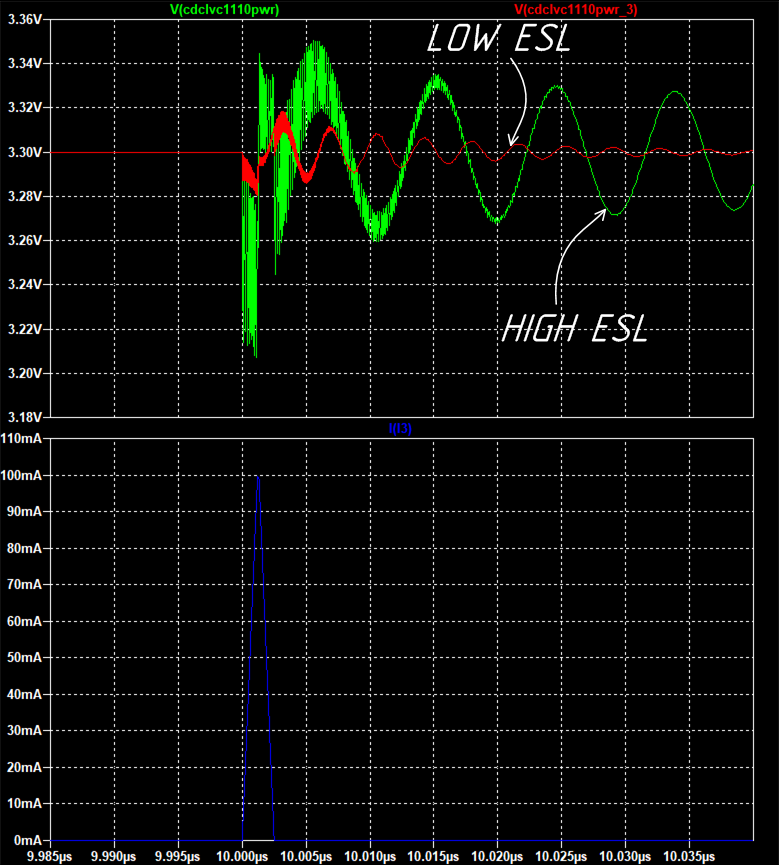
Тут нужно сразу оговориться, когда говорят о ESL, имеют ввиду параметр конденсатора, но как уже говорилось выше, при построение фильтра нужно подходить комплексно, учитывая не только значение из документации, но и качество трассировки. Можно выбрать идеальный конденсатор с очень низким ESL, но при этом не учесть рекомендации при трассировке.

Из осциллограммы выше видно насколько важно обращать внимание на паразитные параметры выбранных компонентов. Однако, выбрать конденсатор с подходящими параметрами не всегда возможно. Ещё раз обратим внимание на осциллограммы. Видно что переходный процесс, возникающий во время импульсного потребления, имеет резонансный характер, это означает что уменьшив добротность резонансного контура, можно и уменьшить амплитуду пульсаций.

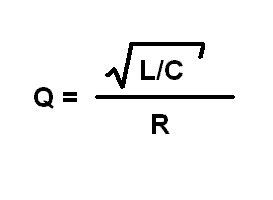
Исходя из формулы, добротность можно уменьшить добавив в контур резистор. В нашем случае мы имеем три параллельных конденсатора, если добавить резистор последовательно с каждым, то мы сильно ухудшим фильтрующие свойства, поэтому добавим сопротивление последовательно с конденсатором у которого самое высокое значение ESL.

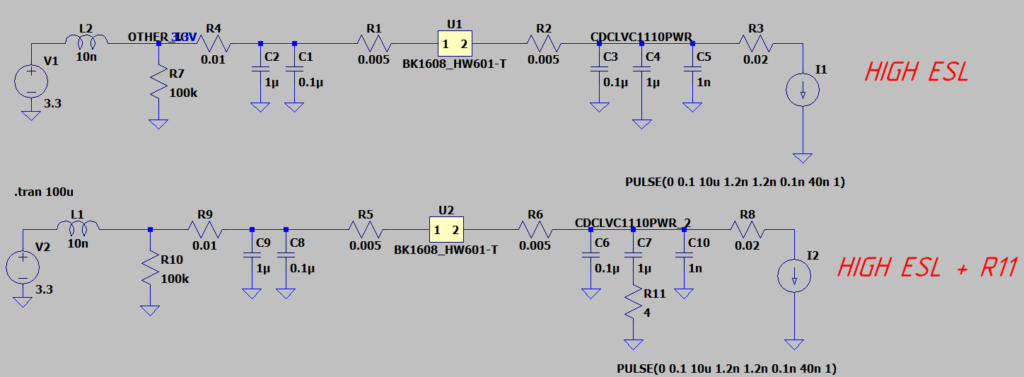
Построим сравнительные осциллограммы.

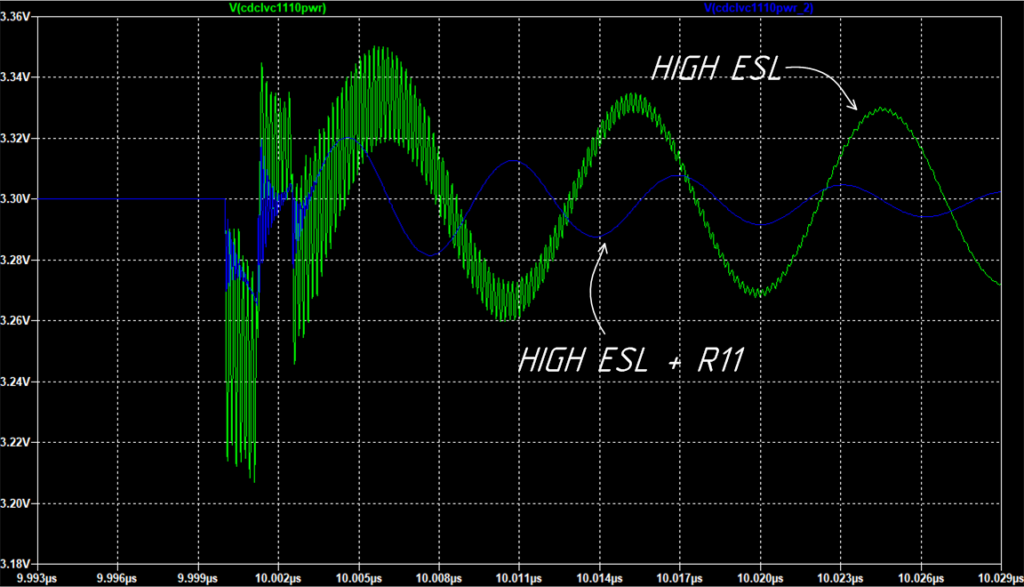
Конечно это не лучший вариант по сравниванию с заменой конденсаторов на меньший ESL, но тем не менее добавление небольшого сопротивления может сильно задавить переходный процесс, сильно при этом не ухудшив параметры фильтра.

Ошибки при выборе ферритовых бусинок.

Для использованной модели мы применяли ферритовую бусинку у которой частотная характеристика, где преобладает R, ложится на область частот от 24Mhz и выше(смотри вторую часть). Допустим заменим применяемую ферритовую бусину на BK0603LL800 и сравним реакцию на импульсное потребление за ферритовой бусиной (в данном примере мы пытаемся защитить шину питания от помех генерируемых микросхемой).

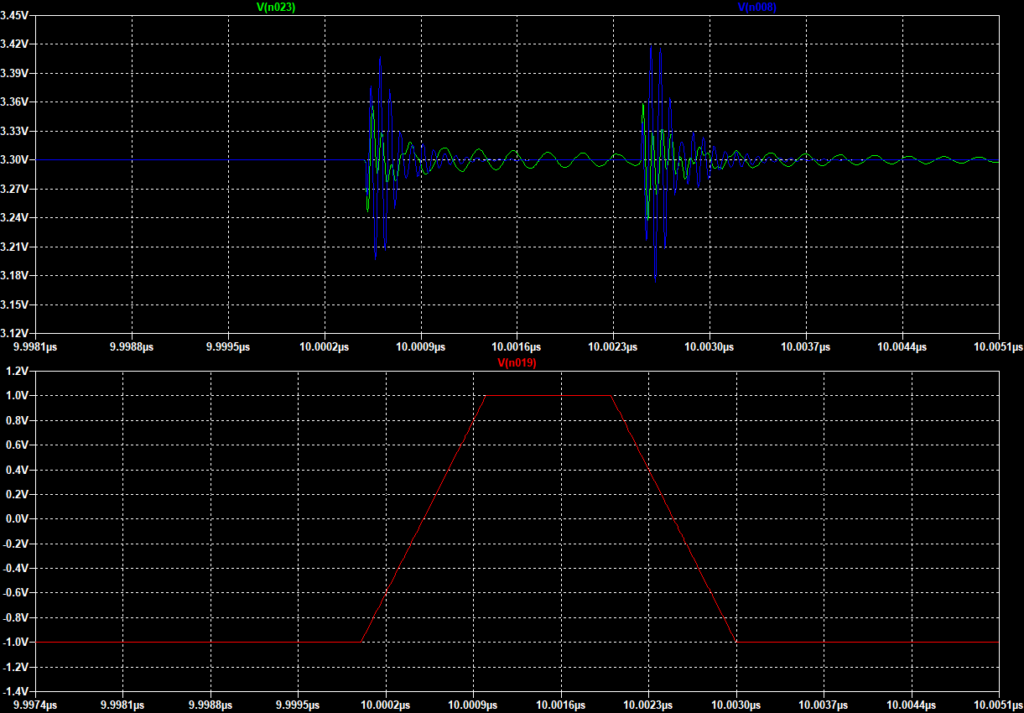
Ферритовые бусины иногда используют и на цифровых линиях передачи. В случае если высокочастотный сигнал передаётся на большое расстояние, неизбежно возникнет звон из за емкостной нагрузки на цифровом входе и индуктивности дорожки(эффект длинных линий не рассматривается).

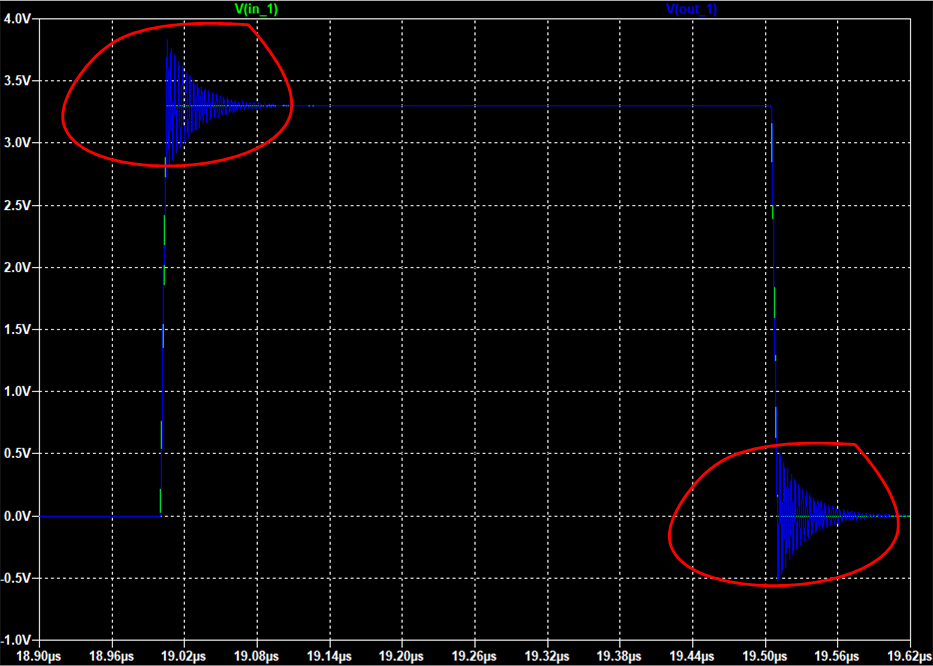
Для борьбы со звоном можно использовать ферритовые бусины. На модели ниже показано три схем. В одной из них не используется феррит, в остальных используется, но в средней схеме активное сопротивление преобладает над реактивным в области частот на которой возникает звон. А в последней наоборот, реактивное преобладает над активным в той же области частот.

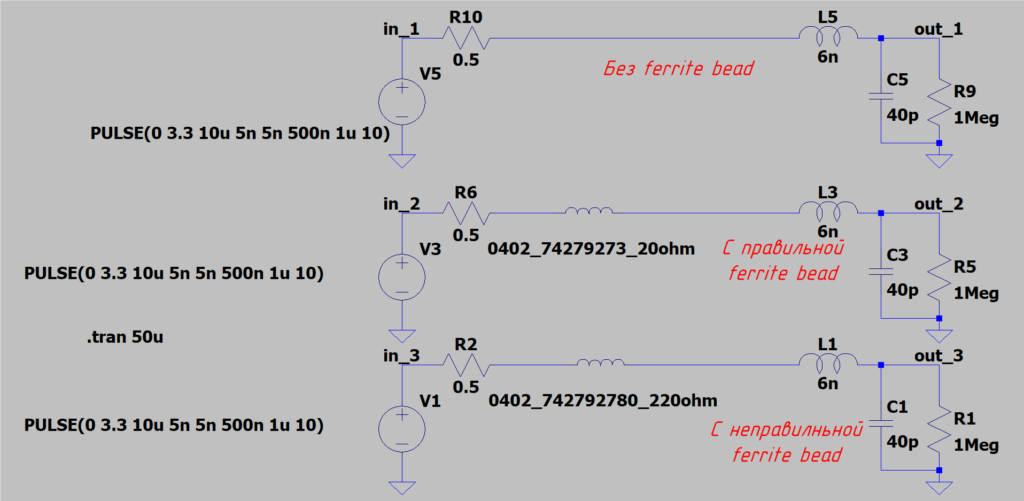
И приведём осциллограммы на выходах out_1,2,3.

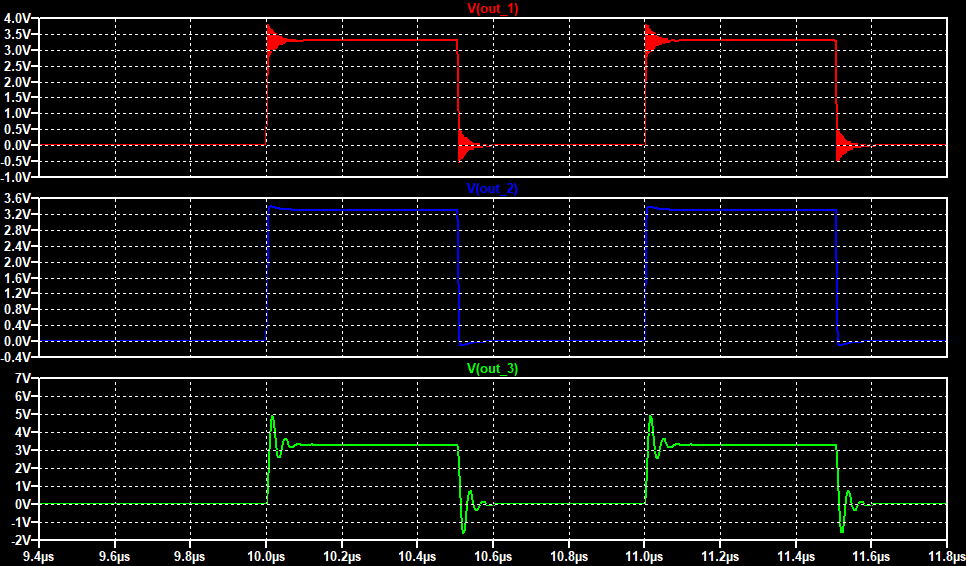
Как видно на средней схеме удалось подавить звон. Применение ферритовых бусин для подавления звона в сигнальных линиях возможно? Да возможно, но тут необходимо быть предельно осторожным. Шаг влево, шаг вправо и вы уже на диаграмме out_3, где подавили высокочастотный звон, но при этом вызвали низкочастотный и с большей амплитудой.

Подавить звон можно и поставив активное сопротивление в линию, какой тогда смысл от бусины? Смысл есть конечно. Из-за её нелинейных частотных характеристик можно подавить звон при этом не ухудшив параметры цифрового сигнала(время нарастания и спада). На мой взгляд, применение активного сопротивления является наиболее подходящим методом борьбы со звоном. В любом случае, на этапе отладки можно поэкспериментировать, запаивая разные бусины на посадочное место резистора, в поисках идеального сигнала.

На этом всё. Модели используемых бусинок можно скачать с сайта wurth и на сайте Taiyo.