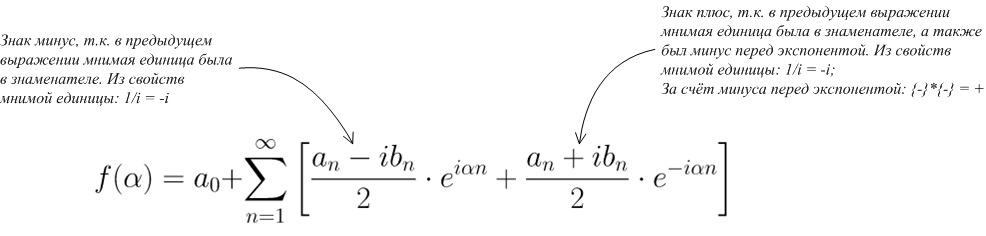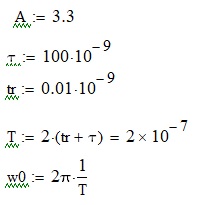Одной из основ signal integrity является понятие спектра сигнала. В данной статье по разберём по косточкам спектр цифрового сигнала, от чего он зависит, как на спектр влияет время спада/нарастания. Для примера будем рассматривать меандр, этот тип сигнала есть почти в любой цифровой схеме и выполняет функцию CLK(clock).

Матчасть.

Для разложения в спектр будем использовать преобразование Фурье в экспоненциальной форме. Почему экспоненциальная, а не тригонометрическая? Дело в том, что когда речь идёт о мнимых числах и длинных математических выражениях, легче работать с степенями экспоненты, чем с тригонометрическими формами, так как экспоненциальный вид записи более компактный. Так же упрощение полученных выражений сводится к алгебраическим действиям, что также облегчает аналитическую работу.

Переход к комплексной форме

Для перехода из тригонометрической формы в экспоненциальную воспользуемся формулой Эйлера:

\Large cos(\theta) = \frac{e^{i\cdot\theta} + e^{-i\cdot\theta}}{2} ; sin(\theta) = \frac{e^{i\cdot\theta} - e^{-i\cdot\theta}}{2\cdot i} (0)

Запишем ряд Фурье в классической тригонометрической форме,а затем воспользуемся формулой Эйлера.

\Large f(\alpha) = a_{0} + \sum_{n=1}^{\infty}\left [ a_{n} \cdot cos(n \cdot \alpha) + b_{n} \cdot sin(n \cdot \alpha) \right ]

Заменяем тригонометрию на экспоненты

\Large f(\alpha) = a_{0} + \sum_{n=1}^{\infty}\left [\frac{a_n}{2} \cdot (e^{i\alpha n} + e^{-i\alpha n}) + \frac{b_n}{2i}\cdot (e^{i\alpha n} - e^{-i\alpha n}) \right ]

Распишем выражение выше на два члена при экспоненте

\Large f(\alpha) = a_{0} + \sum_{n=1}^{\infty}\left [\frac{a_n - ib_{n}}{2} \cdot e^{i\alpha n} + \frac{a_n + ib_{n}}{2} \cdot e^{-i\alpha n} \right ] (1)

Небольшие пояснение по формуле выше

Также можно обратить внимание, что два комплексных числа, стоящих перед экспонентой, являются сопряжёнными числами. Их действительные части равны, а мнимые равны по модулю.

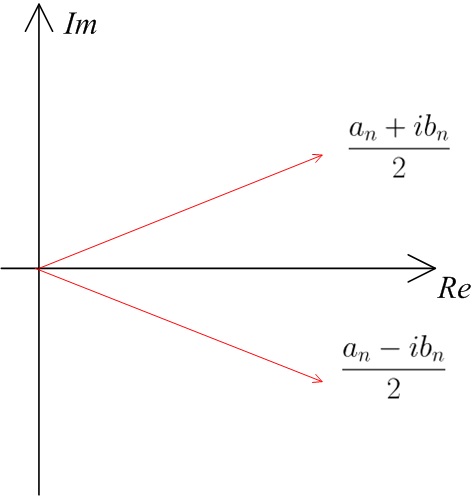
Упростим выражение (1). Можно обратить внимание, что за счёт сопряжённости комплексных чисел можно сделать «реиндексацию» множителей перед экспонентой. Но для начала разобьём общий ряд на два ряда.

\Large f(\alpha) = a_{0} + \sum_{n=1}^{\infty}\frac{a_n - ib_{n}}{2} \cdot e^{i\alpha n} + \sum_{n=1}^{\infty}\frac{a_n + ib_{n}}{2} \cdot e^{-i\alpha n}

Теперь произведём «реиндексацию» во втором ряду, при этом обратите внимание на границы суммы.

\Large f(\alpha) = a_{0} + \sum_{n=1}^{\infty}\frac{a_n - ib_{n}}{2} \cdot e^{i\alpha n} + \sum_{-\infty}^{n=-1}\frac{a_{-n} + ib_{-n}}{2} \cdot e^{i\alpha n}

Теперь мы имеем одинаковые экспоненты, но с разными множителями. Разность множителей заключается лишь в знаках, но так как интервалы тоже имеют разные знаки (в одном случае до плюс бесконечности , в другом до минус бесконечности), мы можем записать всё под один знак суммы, где множитель перед экспонентой заменим на Cn.

\Large f(\alpha) =\sum_{-\infty}^{\infty}C_{n} \cdot e^{i\alpha n} (2)

Обращаю внимание, что сумма включает n=0, именно поэтому в формуле (2) нет коэффициента а0 в явном виде.

Теперь вернёмся к коэффициенту Cn.

\Large C_{n} = \frac{a_{n} - ib_{n}}{2} (3)

Тут an и bn классические коэффициенты ряда Фурье в комплексной форме. Из wikipedia:

Подставив an и bn в формулу (3). Проведя все сокращения, получим формулу для Cn.

\Large C_{n} = \frac{1}{2\pi} \cdot \int_{-\pi}^{\pi} f(\alpha) e^{-in\alpha}

Далее на основе комплексной форме ряда Фурье будем выводить коэффициенты для разных гармоник.

Метод нахождения коэффициентов ряда Фурье.

Для поиска спектра цифрового сигнала воспользуемся методом подсчёта с помощью дельта функции Дирака. Суть метода сводится к пошаговому дифференцированию функции до тех пор, пока она не исчезнет. На каждом этапе !появления! дельта функции вычисляется коэффициент Сn. В конце суммируя Сn от каждого этапа дифференцирования для получение итогового коэффициента перед экспонентой. Принцип по которому складываются коэффициенты от каждого дифференцирования описывается по формуле:

\Large C_n = \frac{1}{jnw_0} \cdot C_{n}^{(1)} + \frac{1}{\left (jnw_0 \right )^{2}} \cdot C_{n}^{(2)} + … (4)

Где C_n_k находится как

\Large C_{n}^{k} = \frac{1}{T} \cdot \int_{0}^{T} \frac{\partial^k f(x)}{\partial x^k} \cdot e^{-jnw_0t} dt

Данный метод поиска вытекает из свойства ряда Фурье: коэффициенты разложения функции x(t) связаны с коэффициентами функции x'(t) (ряд производных) следующим образом:

\Large x(t) = \sum_{-\infty }^{+\infty}C_n \cdot e^{-jnw_{0}t}

\Large \frac{ \partial^k x(t) }{\partial t^k} = \sum_{-\infty }^{+\infty} C_{n}^{k}\cdot e^{-jnw_{0}t}

где \Large C_n = \frac{1}{(jnw_0)^k} \cdot c_{n}^{k}

k — номер производной;
Коэффициент cn под — коэффициент расширения или другими словами амплитуда короткого импульса Дирака (полученная после дифференцирования функции).

Разложение в ряд цифрового сигнала.

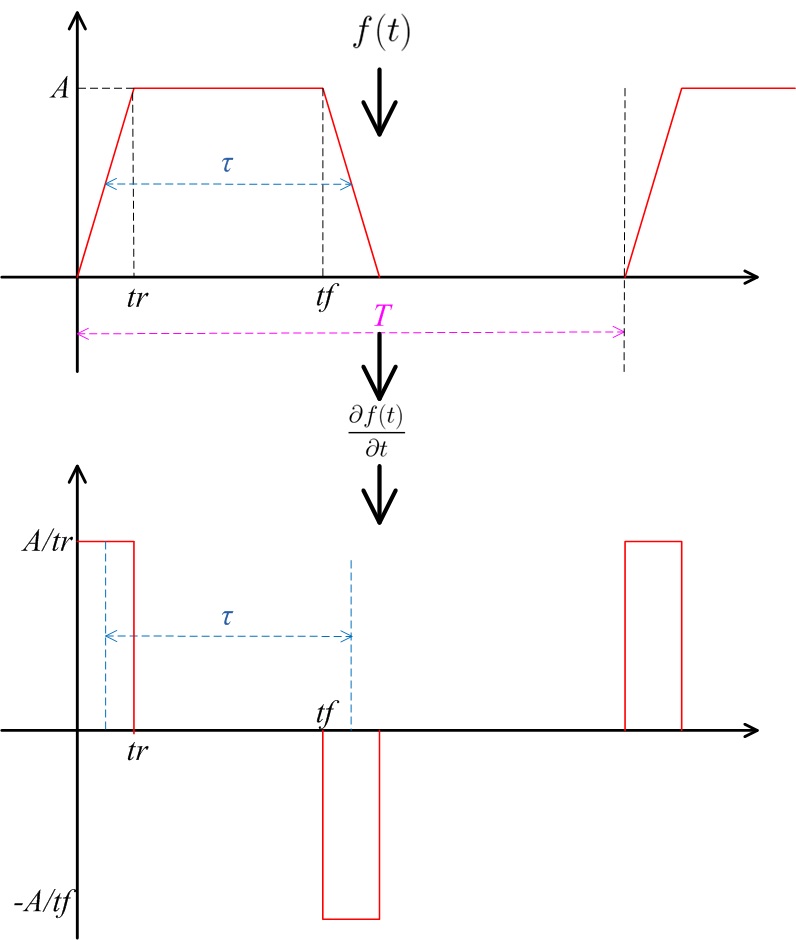
В спектр будем раскладывать цифровой тактовый сигнал f(t) с конечным временем нарастания/спада .

Находим коэффициенты ряда Фурье по методу поэтапного дифференцирования функции f(t).

Коэффициент Сn после первого дифференцирования равен нулю. Это так, потому что df/dt не дало дельта функцию Дирака. Продолжаем дифференцировать дальше.

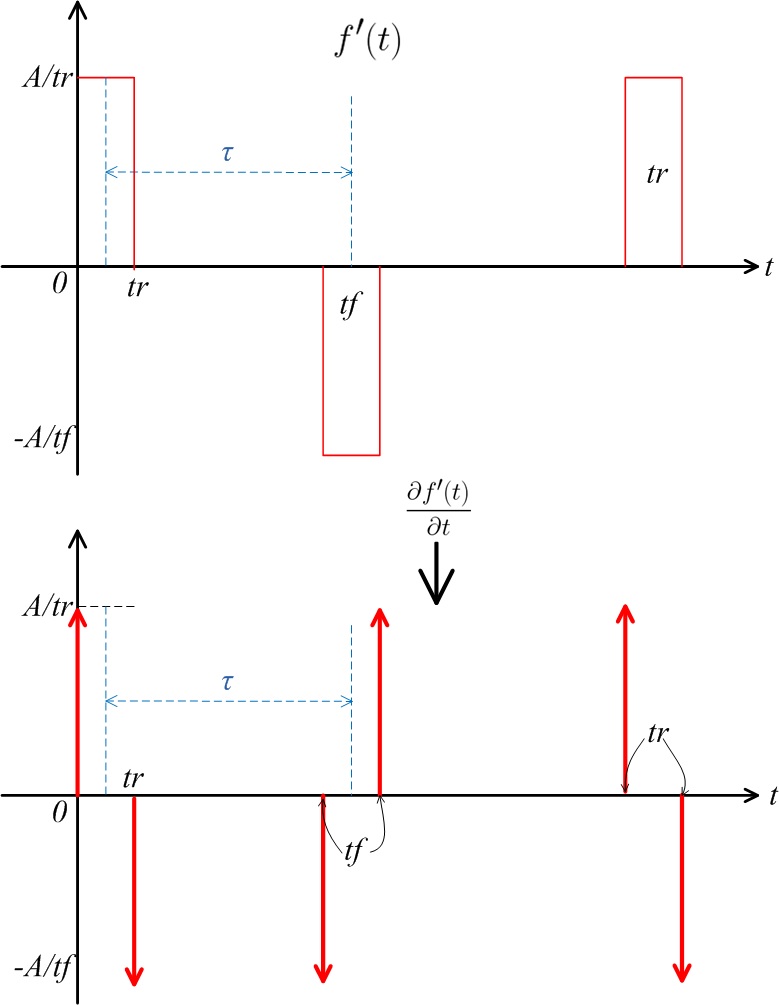
На рисунке стрелочками изображены дельта функции Дирака с амплитудой A/t. Запишем дельта функцию в общем виде:

\Large \int_{0-}^{0+}\delta (t) dt = 1 (5)

Так же запишем важное свойство дельта функции- свойство фильтрации.

\Large \int_{-\infty }^{+\infty}\delta(x+a)\cdot f(x) dx = f(a) (6)

За счёт того, что мы перемещаем «1» бесконечно малой ширины (дельту функцию) относительно x, перемножая дельта функцию на другую функцию f(x), мы получаем выборку функции f(x).

Напоминаю, что общий коэффициент будет складываться по формуле (4). Однако, коэффициента от первого дифференцирования нет (точнее он равен 0).

Теперь найдём коэффициент от второго этапа дифференцирования.

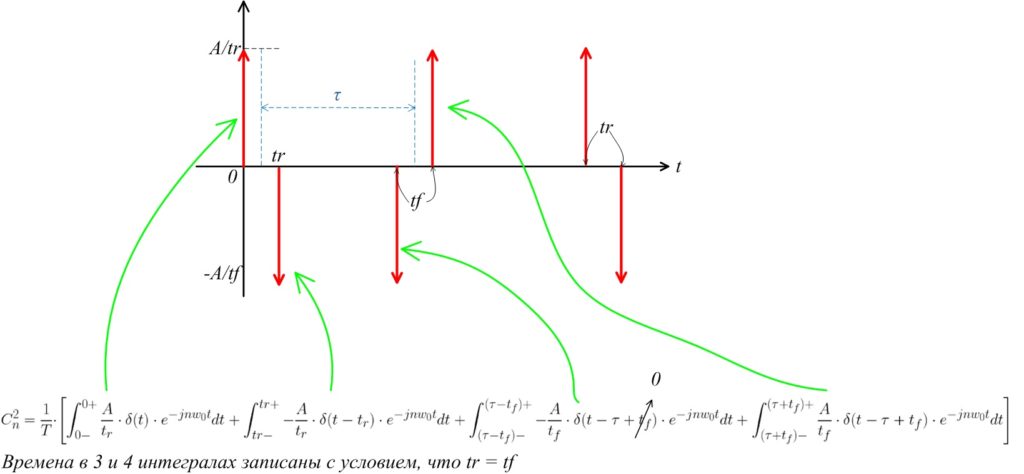
Приступим к упрощению. Применим формулу (5) и (6), а также вынесем за скобки амплитуду А. Сразу примем условие tr = tf.

\Large C_{n}^{2} = \frac{A}{T \cdot t_r} \cdot \left [ e^{0} + e^{t_r} + e^{\tau } + e^{\tau + t_r}\right ]

Вернёмся в начало статьи и вспомним формулу (0). Сейчас наша цель после всех упрощений вернуться обратно к тригонометрической форме. Для этого вынесем за скобку :

\Large e^{-jnw_{0}\frac{t_r + \tau }{2}}

Запишем что получилось:

\Large C_{n}^{2} = 2j \cdot sin(\frac{nw_0t_r}{2}) \cdot \frac{A}{T \cdot t_r} e^{-jnw_0\cdot\frac{\tau + t_r}{2}} \cdot \left ( e^{jnw_0\frac{\tau}{2}} - e^{-jnw_0\frac{\tau}{2}} \right )

Для оставшейся скобки с экспонентой применяем формулу Элейра (0)

\Large C_{n}^{2} = - 4 \cdot sin(\frac{nw_0t_r}{2}) \cdot \frac{A}{T \cdot t_r} e^{-jnw_0\cdot\frac{\tau + t_r}{2}} \cdot sin(\frac{nw_0 \tau}{2})

Множитель -4 получился за счёт перемножения двух мнимых единиц. Вернёмся немного назад и вспомним, что в левой части мы переписали уравнение с учётом этой формулы.

\Large C_n = \frac{1}{(jnw_0)^k} \cdot c_{n}^{k}

И наконец получаем итоговое уравнение для коэффициентов Фурье.

\Large C_{n} = \frac{- 4}{n^2 \cdot w_{0}^{2}} \cdot sin(\frac{nw_0t_r}{2}) \cdot sin(\frac{nw_0 \tau}{2}) \cdot \frac{A}{T \cdot t_r} e^{-jnw_0\cdot\frac{\tau + t_r}{2}}

Упростим формулу и запишем выражение через sinc (домножив и поделив на тау).

\Large C_{n} =\frac{A \cdot \tau}{T} \cdot sinc(\frac{nw_0t_r}{2}) \cdot sinc(\frac{nw_0 \tau}{2}) \cdot e^{-jnw_0\cdot\frac{\tau + t_r}{2}} (7)

Интерпретация матчасти.

Из полученной формулы (7), посмотрим как влияет время нарастания на спектр цифрового сигнала.

Зададимся тактовым сигналом со следующими параметрами:

Как видно, время нарастания tr задано очень малым, в каком-то приближение можно сказать, что это практически меандр.

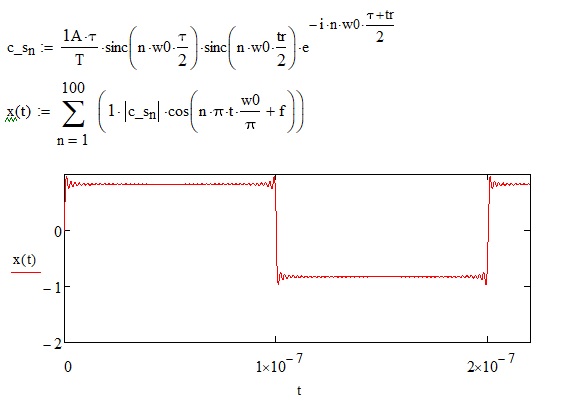
Восстановим сигнал по первым 100 гармоникам.

Построим график распределения амплитуды гармоник в логарифмическом масштабе и подробно разберём его.

Итак, ключевой точкой в данном графике является его начало. Начинается он с частоты 1-ой гармоники или синусоиды, которая больше всего вносит мощности в сигнал. Для наглядности изобразим эту синусоиду на графике восстановленного сигнала.

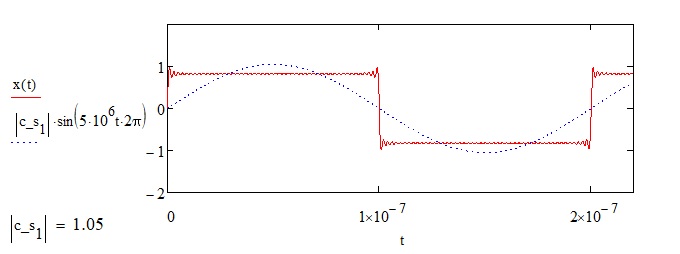
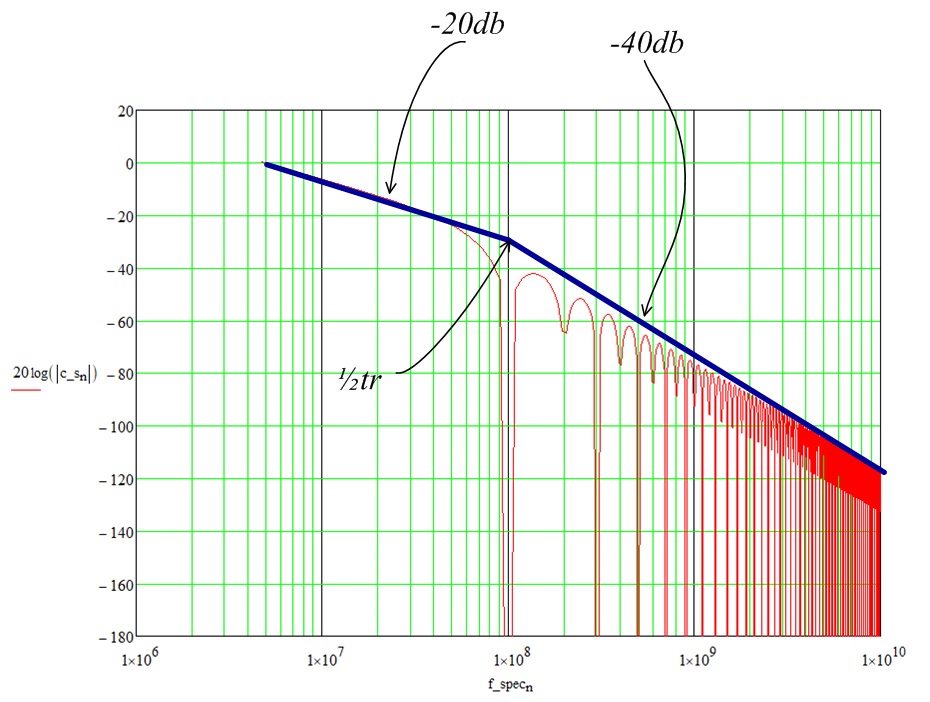
Значение первой гармоники равно 5 МHz. Именно с этой точки амплитуда следующих гармоник начинает спадать со скоростью 20db на декаду.

Если рассматривать сигнал clock с точки зрения перекрёстной помехи (cross-talk), то наиболее страшные высшие гармоники, так как если рассматривать емкостную связь через паразитные конденсаторы, то высокочастотной помехе легче пролезть (вспоминаем импеданс конденсатора Zc = 1/wC).

Затухание -20db не самое быстрое затухание которое можно представить. Другими словами 41-я гармоника примерно даёт затухание в 100 раз. И в случае высокочастотного сигнала clock 41 гармоника будет иметь очень высокую частоту с хорошим cross-talk.

Один из способов увеличить затухание это растянуть по времени время нарастания и время спада. Посмотрим на спектр сигнала из прошлого примера, но с временем нарастания/спада 5нС.

Затухание спектра такого сигнала:

Затухание -40db значительно смягчает требования к трассировке с учётом cross-talk. Именно поэтому иногда следует намеренно применять затягивание фронтов.

Заключение

Разумеется каждый раз при проектирование инженер не проводит расчёты всего и вся практически с нуля, в большинстве случаев достаточно полагаться на опыт и так называемые rule of thumb. Однако, всегда полезно знать, что прячется под rule of thumb 😉